This post is comprised of different sections
Take a look at our review of Flatland: A Romance of Many Dimensions!
Learn more about spatial dimensionality!
This post is comprised of different sections
Take a look at our review of Flatland: A Romance of Many Dimensions!
Learn more about spatial dimensionality!
Author: Edwin Abbott Abbott
Publisher: Seeley & Co.
Year: 1884
Language: English
Country: England
Number of pages: 96

Our rating
Your rating
If I ask you to describe to me a three-dimensional object, none of you will have any trouble doing it, right? “Just look around, dude!” would be a likely response.
And you would be dead right!
Our universe exists in three dimensional space, so we, as part of this universe, are constantly interacting with 3-D objects, and are, ourselves, 3-D objects.
Now, I must warn you that this article will probably stretch your brain like no other. We are going to hop on on a very strange tour in a very strange land with very strange inhabitants…
Dear readers, welcome to Flatland!
Flatland is a story narrated in the first-person perspective of a character called A Square (a literal square), after he had a glimpse of the third dimension.
The novella is split into two parts. In the first part, A Square explains to the reader the different aspects of living in his 2-D world that three-dimensional beings call Flatland: the different shapes that exist, the social hierarchy, particularly meaningful events that occurred, etc.
In the second part of the novella, A Square narrates his (mis-)adventures after a Sphere visits Flatland and takes A Square on a sightseeing tour of Spaceland, allowing A Square to gain an understanding of three-dimensional space.
I find the idea of Flatland spectacular. For a novel written in the late 1800s, Flatland seems impressively contemporary in its ideas and it has managed to remain relevant even to this day.
Indeed, plenty of films and TV shows have direct references to the novel. For example, in the film Interstellar (which is related to the concept of higher-dimensional space), Joseph Cooper accidentally drops the novel Flatland from a bookshelf. In the TV series The Big Bang Theory, Sheldon Cooper mentions that one of his favourite places to visit is Flatland from Abbott’s novel.
Abbott, who had graduated with the highest honors in mathematics, showed that he knew his business. His descriptions of places existing in lower dimensions were picked by the likes of Stephen Hawking and Carl Sagan, who took inspiration from Abbott’s novella and popularised the topic of extra dimensions.
Despite its potential, I do have a few criticisms.
First, the first part of the novella (which comprises half of the book) is purely descriptive of the inhabitants and the world they live in. There is no particular plot to speak of. Even the second section of the novella, which is certainly the most interesting of the two, suffers from an underdeveloped plot, with only sporadic and ephemeral entertaining passages.
Thus, even though I found the topic of dimensionality extremely interesting, it felt more like reading a textbook rather than a novella.
The writing style of the first section in particular was also quite difficult for me to get into. In all honesty, I learnt more about the topic from reading reviews of the book than from the book itself. That might sound unfair, given that we had more than 100 years to dissect Abbott’s novella and apply modern teaching tools to explain dimensionality.
Nevertheless, it could have been written in a more reader-friendly and exciting way, as some science fiction books from some of Abbott’s contemporaries (e.g., Jules Verne, H.G. Wells). Abbott’s descriptions were often convoluted and off-track, and I found myself losing interest quickly (although his explanations improved in the second section).
I did, however, find his drawings amusing, and they did help visualise the second dimension much more than the text descriptions were able to.
I have to say that I have mixed feelings regarding Flatland.
On the one hand, the topic was great. Also, taking into account that the book was written at the end of the 19th century, I do think Abbott was reasonably good at simplifying a very complex topic to non-mathematicians (particularly his drawings).
However, the writing style and the descriptions of the first section were just not my cup of tee, and I think the book could have been improved to be a more interesting read.
Since Flatland is a novella, I was also expecting a relatively interesting plot. However, plot was almost inexistent, with most of the book devoted to explaining dimensionality. The most exciting event was A Square’s interactions with the Sphere, which really took up only two chapters.
Here at Mindlybiz, Flatland gets a rating of 2.5.
Hmmm… I would say Flatland is bizarre, not for the obvious reasons that the all characters are geometric figures (which is kind of weird on its own), but because the novella is highly satirical in tone.
Also, the topic of dimensionality is not an easy one to grasp, although I think the author did a relatively good job simplifying it to the general, non-mathematician reader.
Flatland gets a bizarrometer score of 2.
It is possible that Abbott wrote Flatland with two aims in mind: 1) as a gentle introduction to the concept of spatial dimensionality, and 2) as a criticism of the social stratification that prevailed in the Victorian society of his time.
With respect to spatial dimensionality, Abbott chose to write his novella from the first-person protagonist narrator A Square, an inhabitant of a two-dimensional (2-D) world called Flatland, where 2-D geometric figures are organized in rigid social classes.
After describing the inner properties of Flatland and its inhabitants, A Square visits Lineland (a 1-D world) and has a conversation with its King. The King of Lineland could only see A Square (and everything else) as a single point, and had no understanding of the left-right dimension, since his 1-D world restricted his movements to only North-South directions. Witnessing the simple life of the King of Lineland, A Square pities the King and arrogantly concludes that his 2-D world is the true world.
Later in the novella, A Square meets the Point, the only being in Pointland (a 0-D world), who couldn’t conceive anything existing but his own self. Even when he heard A Square’s voice, the Point thought the voice was coming from his own mind.
With the arrival of the Sphere to Spaceland however, A Square begins to understand the limits of his own existence. The epiphany that there is another world beyond Flatland leads him to drop any previous assumptions that Flatland is all there is. In fact, he goes further and claims that even higher dimensional worlds than Spaceland must exist, something that even the Sphere quickly dismisses.
Abbott was very critical of blindly basing one’s faith on miracles, so perhaps he was pointing out that we should not haste attributing powers to phenomena we cannot understand. The Point, the King of Lineland, A Square and the Sphere all refused to accept the possibility of superior planes of existence, because their restricted dimensionality prevented them from visualizing these extra dimensions. In a twist of irony, when A Square finally becomes aware of the limitations of Flatlanders’ minds, he transforms himself into an almost biblical prophet, preaching the Gospel of the third dimension, even if that meant certain incarceration.
In addition to teaching about spatial dimensions, Flatland appears to have been written as a social satire. Having lived in the mid-late Victorian era, a time of strict class rigidity, pervasive misogyny, sexism, and oppression of the working class, Abbott felt the need for deep societal changes. Flatland was likely his response to these issues.
The appalling descriptions of women as lacking intelligence, sense of justice and reason probably echoed the attitudes of Victorians towards women. The working class was also viewed as simply factory fodder, too easy to manipulate and replace whenever their utility declined. The clergy held an enormous control over people, and remained a powerful influence on state affairs, particularly on education and policymaking. All these aspects of the Victorian society are in some way or another satirized in Abbott’s novella.
So, that’s Flatland in a nutshell. Let’s now go over some really interesting facts about dimensions, because they will come in very handy when discussing Abbott’s book.
When you think of dimensions what comes to mind?
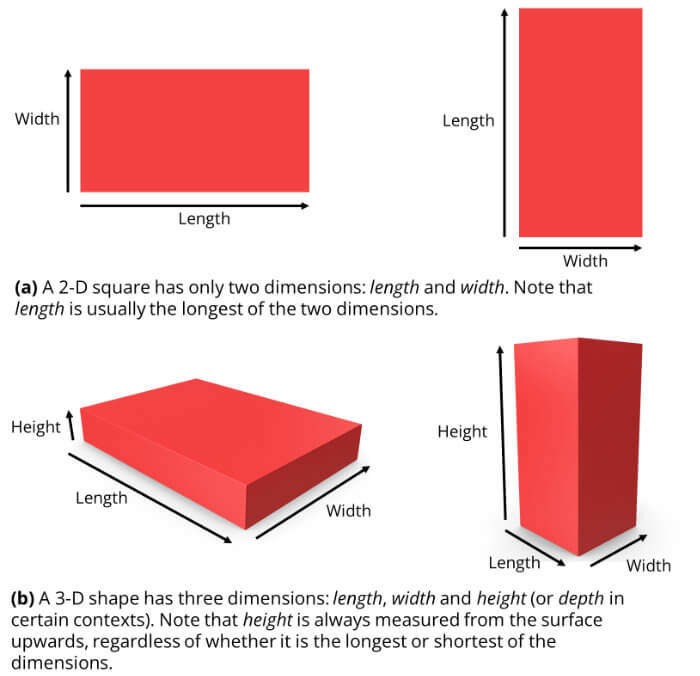
When I hear the word dimension I immediately think of the measures of length, width and height. For example, when I want to describe the size of a shoebox (i.e., to know its dimensions), I say it’s 30 cm (12 in) in length, 20 cm (8 in) in width and 15 cm (6 in) in height.
Length, width and height are especially meaningful because we can describe the size of pretty much every object simply by defining these dimensions. And using the size of an object is equivalent to say how much space that object takes up in our world.
If you understand that idea, then you are in a very good position to understand the quirks of Flatland.
But let’s start from the very beginning. You know our universe is three-dimensional. But, can we imagine what a lower dimensional object might look like?
The only object that has 0 dimensions is a point. But as in all things “mathematical”, we need to be very precise how we define a point.
Whenever people think of a point, they will imagine something like this • . But that isn’t 0-dimensional. It’s actually two-dimensional, because I can tell that it has a bit of length and width, say 1 mm x 1 mm (see figure on the left above).
A 0-dimensional point is an infinitesimal point. It has zero length, zero width and zero height, and, thus, cannot be measured with existing tools.
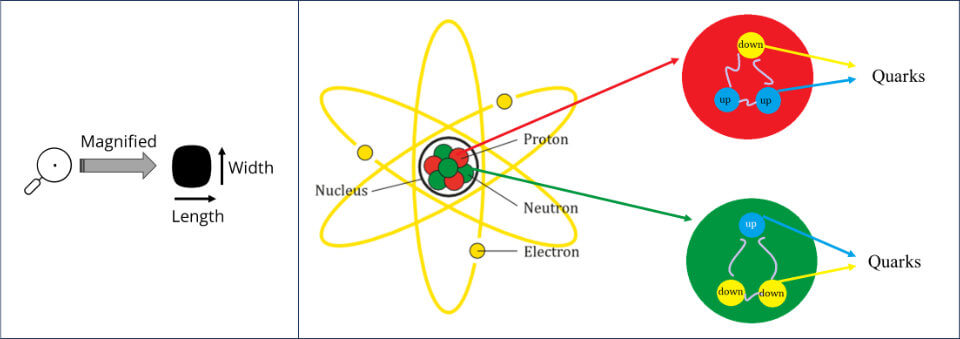
You might reasonably argue that a 0-dimensional point then simply doesn’t exist. And, yes, 0-dimensional points do not exist in reality (at least, not in our reality) – they are a purely theoretical construct.
Bear in mind, however, that some scientists have suggested that point-like particles such as quarks and electrons may be zero-dimensional (see the above figure on the right), but that view is not unanimously accepted.
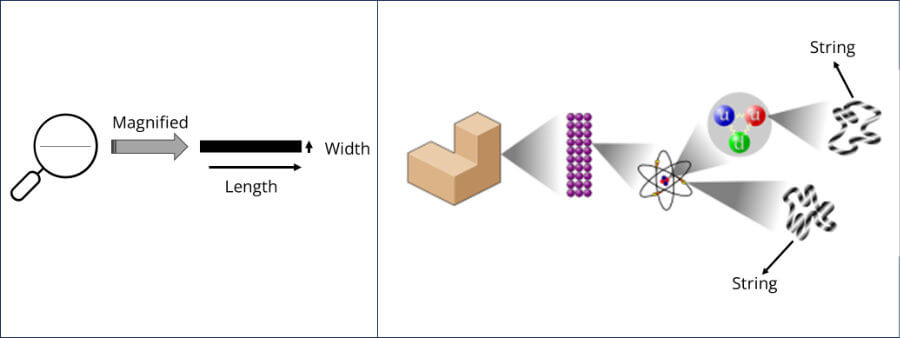
OK, now imagine you had a bunch of those infinitesimal 0-dimensional points and connected them. What would you get?
A line!
Again, not a line like this — (that’s a two-dimensional line, because it has length and width, see the above figure on the left), but a line with only length as a dimension.
To state the obvious, a one-dimensional line has only one dimension, which is its length, and it has 0 height and 0 width.
How would a one-dimensional line look like in our world? Well, can you picture a line without width and height? Likely not.
So, as with 0-dimensional points, one-dimensional lines do not exist in our universe. Some physicists theorise that the strings postulated by string theory may be one-dimensional, although there is no scientific evidence to back it up.
Now what about two dimensions? In most cases, people will tell you that a square drawn on a sheet of paper is two-dimensional because it has only length and width.
However, that is technically incorrect.
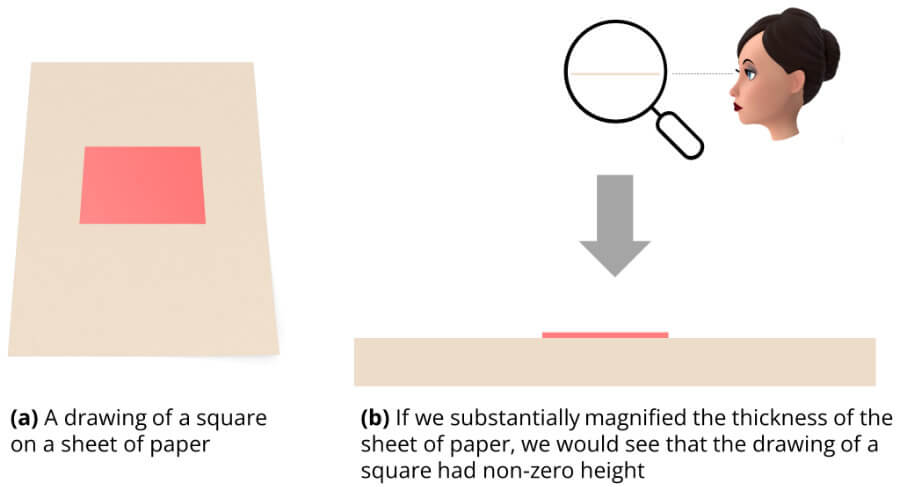
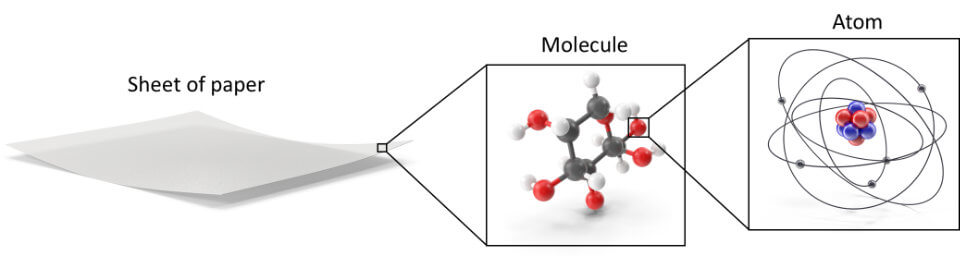
The square you draw on a piece of paper isn’t two dimensional because it too has a bit of height. No matter how flattened your drawing of a square is, if you had a potent microscope and zoomed in on your drawing, you could see that it had a tiny bit of height as well (see figure above).
Graphene, a material made of pure carbon, is also usually described as a truly 2-D object. However, even though graphene is the thinnest possible object since it is exactly one atom thick, it is still three-dimensional, because atoms are themselves three-dimensional.
Nevertheless, scientists are happy to ignore its thickness, since, on the one hand, it is negligible, and on the other, it is likely the closest thing to a 2-D object we will possibly ever get.

It is more accurate to think of a square drawn on the computer screen as a truly two-dimensional square (a shadow has also two dimensions). But again, we need to be careful with the kind of labels we give to these things. A square on the PC monitor (just like a shadow) isn’t really an object – it doesn’t interact with our world, so it does not take up any space.
And that is a really important point here. Could a 2-D square ever exist in our 3-D world?

Let’s imagine we could take the square drawn on the PC monitor and somehow represent it on our 3-D space. The square wouldn’t have height, so if you tried to measure its height with the most potent of microscopes, it would appear as though it disappeared. But then, you would look at it from above and it would suddenly appear (see figure above).
So weird!
Because this sounds like an impossibility and defies the laws of physics, truly 2-D objects are unlikely to exist in our 3-D space.
So what kind of objects have three dimensions? This should be easy-peasy: everything!
That’s right! Every physical object that exists in our universe has three dimensions. That’s because atoms, the stuff of all matter, are themselves three-dimensional. And what makes an object three-dimensional? Well, the ability to describe its size using the three dimensions of length, width and height. And if an object has non-zero values in all of these dimensions, then it takes some amount of space in our world.
We could extend the argument that adding another dimension to those three would allow us to represent an object in 4-D. What would that object look like? Hah! That is a topic for a whole different article coming up very soon!
Great! Having established that objects with less than 3 dimensions cannot possibly exist in our world, let’s now ask the reverse question. Could a 3-D object exist in a 2-D world?
Now, based on what I said above that all atoms are three-dimensional, it would be impossible to reduce atoms to two dimensions without collapsing its atomic structure. No biological and chemical interactions as we know them would be possible, and no matter would be formed, so it’s clear that we could not exist in a 2-D world.
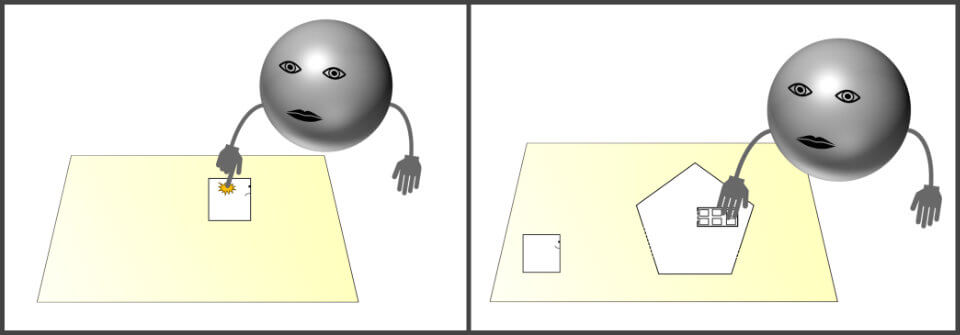
Still, for the sake of fun, let’s imagine you could get inside the computer screen, how would 2-D beings actually see a 3-D object?
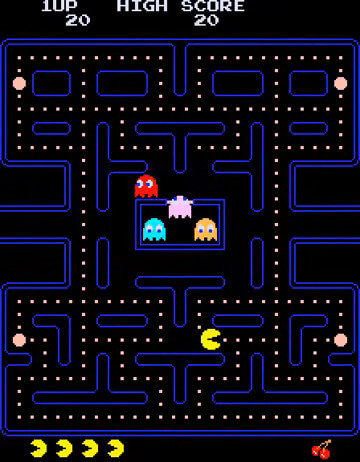
For this exercise, I’d like you to think of the original 1980 game, Pacman (see figure above).
As we have established above, the images on a computer monitor could be thought of two-dimensional, so we could consider Pacman and the fiendish ghosts as two-dimensional objects.
Why? Well, would you be able to pull the original Pacman off the screen and into our 3-D world?
No, not really.
Don’t fool yourself thinking that if you removed Pacman from the screen, he would somehow acquire the shape of a sphere in our world. Again, 2-D Pacman would have no thickness so it wouldn’t be able to exist in our 3-D world, since we could not represent Pacman’s height.
But what if a human were to cross Pacman’s land?
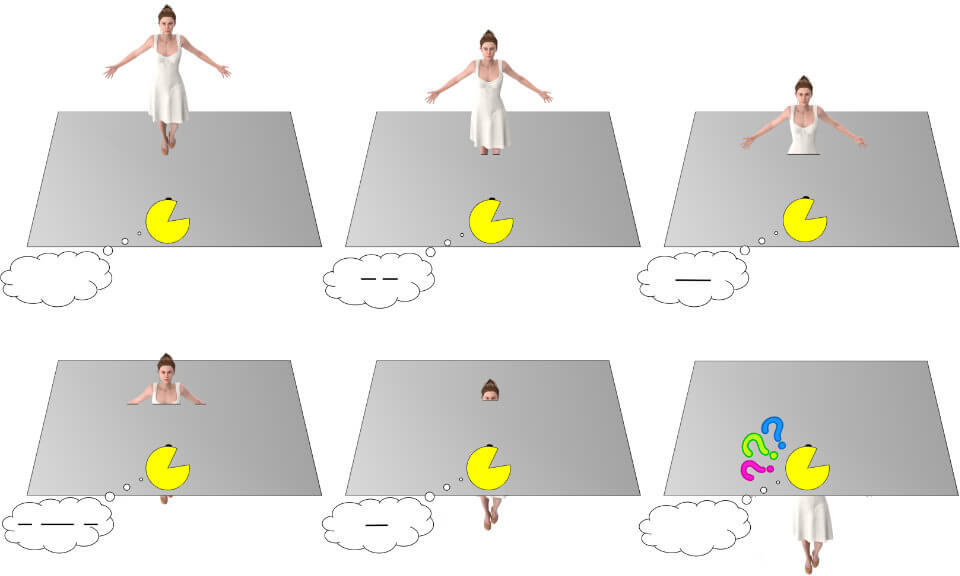
If you look at the figure above, where a 3-D woman is interacting with Pacman’s 2-D world while falling down, you will have an idea. Pacman would essentially only see a cross section of the woman, the section that is interacting with his 2-D world.
But, since Pacman has no concept of height, he is unable to differentiate the different cross sections of the woman. To him, every cross section is the same, a bunch of lines.
But remember, even though I represented the cross section of the woman entering Pacman’s world as a black line (which is a two-dimensional line because it has length and a bit of width), Pacman would actually only see a one-dimensional line (i.e., 0 width and 0 height, only length).
Alas, I cannot depict a one-dimensional line on the screen, as it would be invisible to our eyes… but not to Pacman’s eyes.
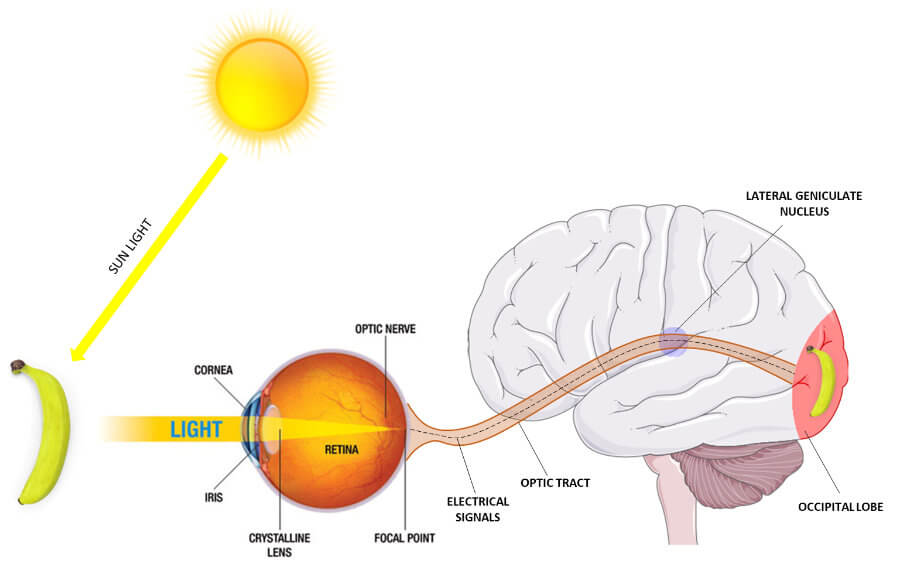
And that brings me to a crucial point.
Our vision is possible because light reflected off objects enters our 3-dimensional eyes and converges on the retina in each eye. The retina contains photoreceptors (rods and cones) which convert the incoming light into electrical signals that are then sent to the occipital cortex. The occipital cortex processes this information, allowing us to “see” in 3 dimensions.
Colloquially, we tend to speak of our vision as 3-D. Even textbooks will tell you that our brains convert the electrical impulses from both of our retinas into a stereoscopic 3-D image.
However, that is technically incorrect. If our brains were truly capable of generating a pure 3-D image, we would be able to see the back of the objects that are usually occluded from our sight.
It is perhaps more accurate to say that we possess 2.5-D vision. That is, we see two-dimensional images with the addition of the illusion of depth.
Right. The problem is that Pacman has no 3-D eye or 3-D brain. Both his eye and his brain must be two-dimensional.
If incoming light from objects form 2-D images using our 3-D eyes and brain, we can extrapolate that 2-D objects would be projected as a 1-D object on Pacman’s retina, and so Pacman would see in 1-D (or maybe in 0.5-D; check Do we really see in 3-D? Not really, more 2.5-D.).
And what is a 1-D object? A line, of course.
Flatland is as much as a treatise on geometry as it is a satirical work. It instructs us in space dimensionality, while implicitly pointing out serious social issues in Victorian Britain.
I will begin this section with a summary of the characteristics of the world of Flatland, its inhabitants, and A Square’s (mis)adventures in lower and higher dimensions.
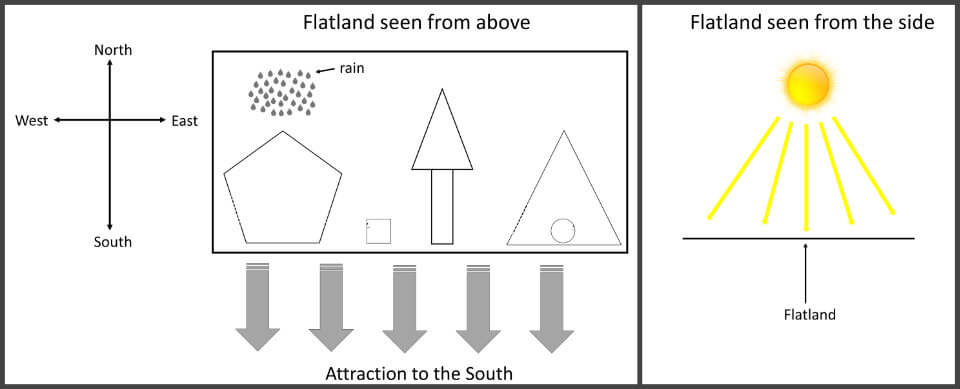
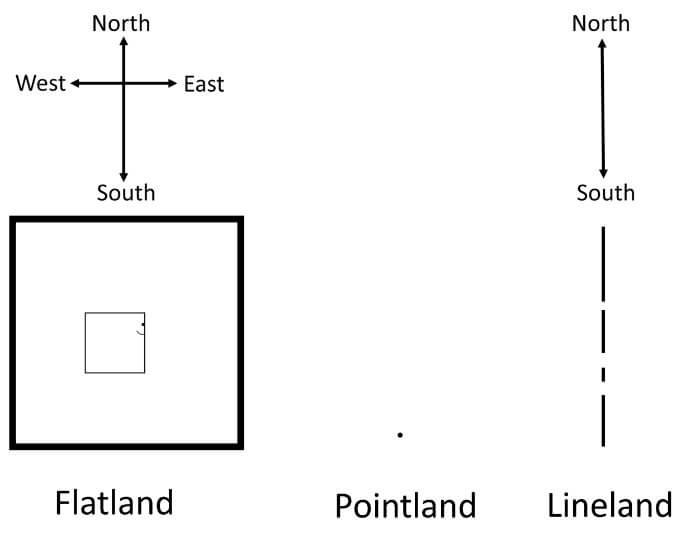
Flatland is a 2-D world, which the narrator, A Square, equates to a vast sheet of paper on which the 2-D inhabitants (geometric figures, see below) move about.
Houses in Flatland have no windows, because light shines the world at all times. Inhabitants are forbidden to question where the light comes from. Of course, the light comes from the sun which Flatlanders cannot see since they cannot access the third dimension (see figure above).
Flatlanders can travel North, South, East and West, but because they do not see the Sun or the sky, they discern direction by other means. For example, rain in Flatland always falls from the North; Flatlanders have a natural attraction to the South; and the tree tops always point to the North. These occurrences give the inhabitants of Flatland the ability to tell direction.
Most houses in Flatland are pentagons (five-sided shapes), with only government buildings being triangular. The roofs of the houses also point northwards.
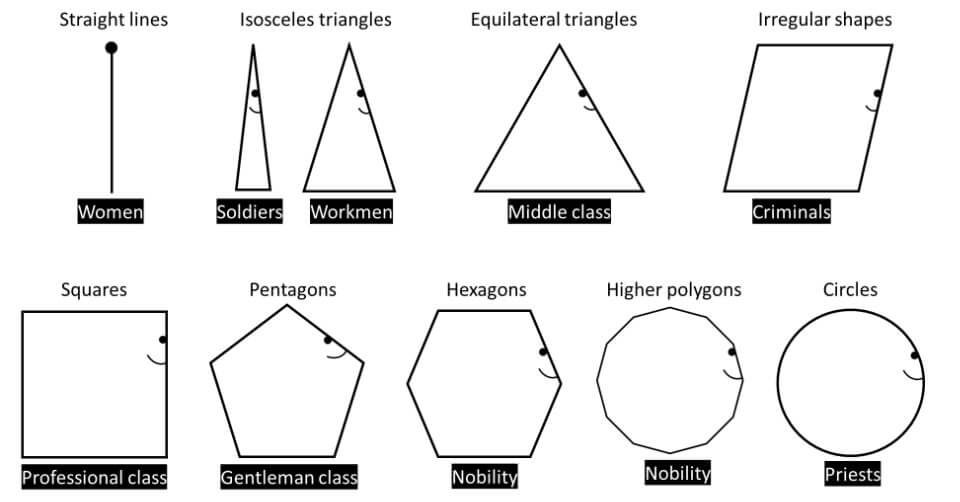
The world of Flatland is inhabited by seven types of geometric figures no longer or broader than 12 inches (30 cm):
Straight lines in Flatland comprise the women. One of the two endpoints of the line is the eye, which is painted, whereas the other end isn’t.
Women in Flatland are terribly marginalized. They are considered inferior to men, too emotional and lacking intelligence, reason and judgment. They are forbidden to receive any type of education, so they cannot read, write or do mathematics.
They are also viewed as highly dangerous. Because they suffer from really bad memory, when frustrated and angered, they are capable of murdering their husbands and sons without later recollecting any of it.
In addition, their pointed extremities, much like a needle, also worries Flatlanders, which led the government to prescribe laws to protect its male citizens. For example, in order to avoid deadly collisions, women must enter houses via a small door located East, and must constantly hum a Peace-cry in public to let others know of their presence. Women who are ailed with a condition that causes them to make involuntary movements are destroyed on the spot. In certain places in Flatland, Women are not even allowed to stand still, and must be constantly swaying their backsides from left to right.
These shapes are the soldiers, working class men and, occasionally, criminals.
Isosceles triangles have sides which are not equal (base is smaller than the sides). This characteristic is looked with disdain by the higher classes, and they are barely considered human with an almost lack of intelligence.
These shapes are the middle class and tradesmen. Equilateral triangles have all sides equal to each other.
These shapes are the professional men and gentleman class (e.g., lawyers, physicians, etc.). Both squares and pentagons have equal sides, but broader angles than equilateral triangles.
To this class belong the nobility men. They are well-educated and intellectual individuals, who aim to become Circles.
Circles consist of Priests. They are actually not real circles, but polygons with hundreds of tiny sides, so small that make them look like circles. They essentially regulate all aspects of life in Flatland by dictating the laws, and controlling business, art, science and theology.
While the number of sides vastly grows with each generation, so does infertility. Thus, Circles with more than 500 sides rarely have sons, but when if they manage, their sons will have way more sides than their fathers. The closer to a perfect circle, the more prestige a circle has.
These shapes comprise all of those whose configuration deviates from that of any other inhabitant (be it a line, a square or a circle). Irregularity is seen as a disease in Flatland, and irregular shapes are either killed or manipulated at birth.
Irregulars are often ignored by society, they are forced to work in low-wage jobs and are not allowed to marry or to produce offspring. For these reasons, they often turn to crime to survive.
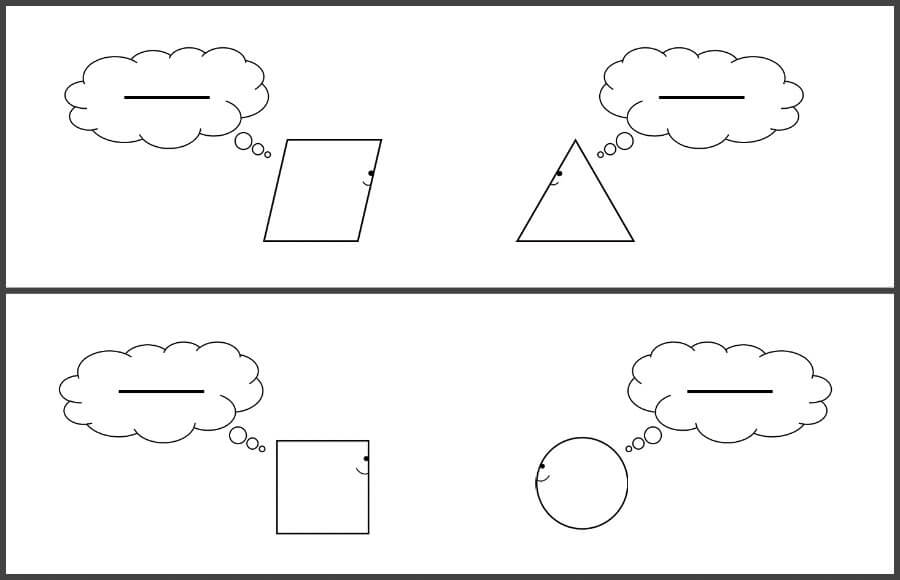
As you have learnt in section Sightseeing in Pacman’s land, Pacman, a 2D figure, can only see lines.
Well, this happens to apply to every single inhabitant in Flatland, who are only able to see lines, regardless of the actual geometric shape. Whereas our vision allows us to use shade, colour and perspective to differentiate among objects, flatlanders can use no such aids.
For a world based on a strict hierarchical social structure, this limitation naturally poses problems.
Sometimes individuals can be recognised by sound. Individuals from lower classes, such as triangles and squares, can detect subtle changes in tone and inflection to distinguish an individual’s class. However, aristocratic shapes do not seem to have this ability as their sense of hearing is much poorer.
Another popular method is the sense of touch, who is more often used by women and the lower classes. For example, by tracing out the sides of the shape, an individual could infer the type of shape in front of them based on the angles its sides make.
However, as the number of sides becomes larger, the ability to discern shapes diminishes – for example, a 20-sided shape might be confused by a 24-sided shape. There is also the risk of injuries when shapes have very sharp angles, such as Isosceles triangles.
The third method of recognition is that of sight. Even though every Flatlander can only see line segments, an atmospheric phenomenon called “Fog” enables Flatlanders to perceive distance. Objects, or parts of an object, that are further away will tend to disappear into this dense fog.
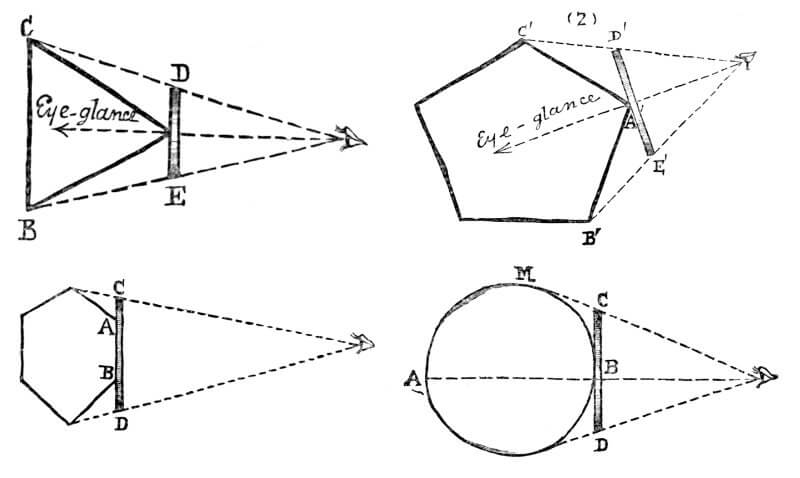
Take a look at Abbott’s drawing above, which includes an equilateral triangle (upper left), a pentagon (upper right), and hexagon (lower left) and a circle (lower right).
If an individual sees an equilateral triangle with its pointy tip facing the viewer, its sides will disappear quickly into the fog, because equilateral triangles have very sharp angles. In contrast, if the figure is a pentagon with broader angles, its sides will fade away less quickly, and will look brighter.
The science and art of recognition by sight is taught exclusively to the elite at universities, and is, therefore, the preferred recognition method by the higher classes.
Aesthetically, Flatland looks quite dull. Art consists of nothing more than straight, coulorless lines.
However, it was not always like that. In a distant past in Flatland’s history, an ancestor discovered colour and painted himself, his family and his home. Soon, many Flatlanders started to realise the benefits of colour, specifically for distinguishing different shapes, as different shapes could be painted in different colours.
The act of painting quickly spread through Flatland, initiating the Color Revolt.
Art and poetry flourished, whereas intellectual endeavors diminished in importance. Sight by recognition fell into disuse.
Only Circles and Women were not painted. The revolutionaries, however, started to demand that Circles and Women be painted in the exact same colours (half red, half green). This idea was prompted by a desire to bring down Circles’ reign over Flatland, as it would make it impossible to distinguish a Circle from a Woman. Women were, initially, favourable to the Universal Color Bill, because it meant that they could now be treated like a Circle.
Lower classes also begun to realise that there was not much difference between them and higher classes, so they demanded equal rights for every shape.
Now Circles really began to worry.
A war ensued where the Polygon army was defeated by the ever-growing Isosceles soldiers. The population of Circles also saw a decline because their wives, out of frustration for their husbands’ reluctance to support the Bill, began to murder them.
Just when everything seemed to be heading towards a massive defeat of aristocracy, an Isosceles triangle, painting himself as a higher-class dodecagon, tricked the daughter of a noble Polygon into marrying him. When she found out the truth, she committed suicide.
This pivotal event led many women to start opposing the Bill, for fear of being similarly deceived. The Circles took the opportunity to stir up fear among the lower classes. They did so by leading them to believe that accepting the Color Bill meant that their children would never be able to advance to higher ranks, since class would be abolished for good.
Another war ensued, where infighting among the lower classes led to the demise of all revolutionaries, putting an end to the rebellion. The Circles, now again in full control of Flatland, became even more despotic. They banned colour and enforced even more restrictive measures, such as the killing of any triangle suspected of irregularity, and “home visitations” meant to purge any excess of triangles.

A Square then reveals that he had a dream about encountering Lineland, a one-dimensional space where only lines (men) and points (women) inhabit and move in one single direction.
He converses with the King of Lineland, who explains that the inhabitants’ relative positions to one another are set for life, since they can only move in straight (one-dimensional) lines. The Monarch further explains that Linelanders can only see dots and tell each other apart by voice. Even marriages and the birth of children are done via voice.
A Square disparages the King and his assertion that his universe is all there is. He tells the King that there is another dimension that Linelanders cannot see, but the King refuses to accept that something outside the universe of Lineland exists.
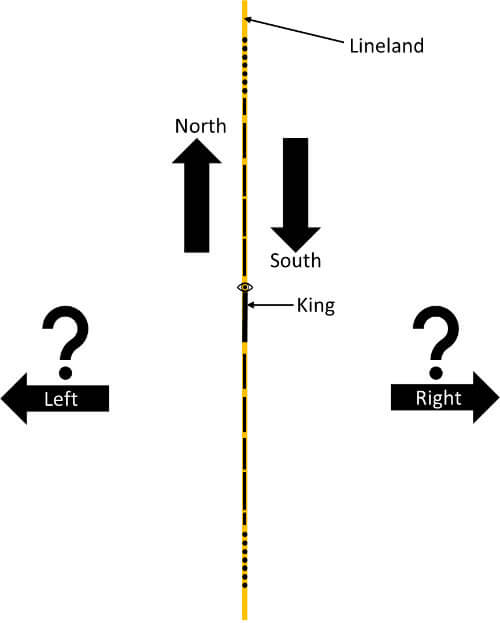
At some point, A Square mentions “left” and “right” which are, obviously, alien concepts to the King of Lineland since, in his one-dimensional world, there is only North and South. Failing to explain with words, A Square attempts to demonstrate it by moving in and out of Lineland. A confused King accuses A Square of using Magic and attacks him after A Square’s bouts of anger, at which point A Square wakes up.
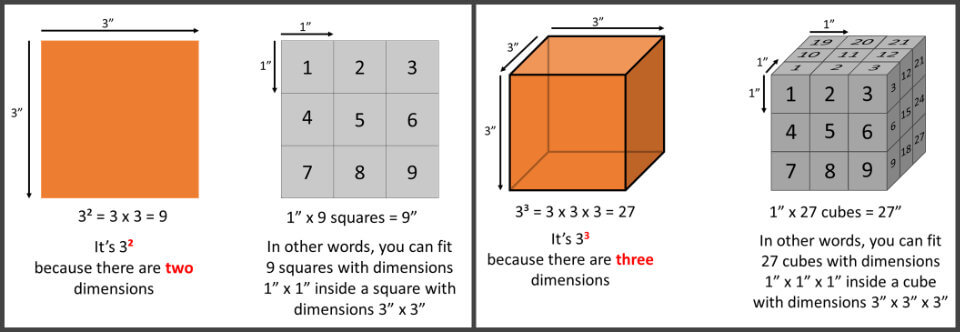
At home, A Square is teaching geometry to his grandson, a talented Hexagon. He explains that one can calculate the area of a square whose sides are 3 inches long by multiplying raising 3 (the length of one side) to the second power (3² = 9 inches).
The grandson cleverly questions if 3 to the third power has any geometrical meaning (3³ = 27). His grandson is, of course, alluding to the third dimension, which would form a cube (see figure above), a concept which A Square cannot picture.
Upset by his grandson’s preposterousness he sends him to bed.
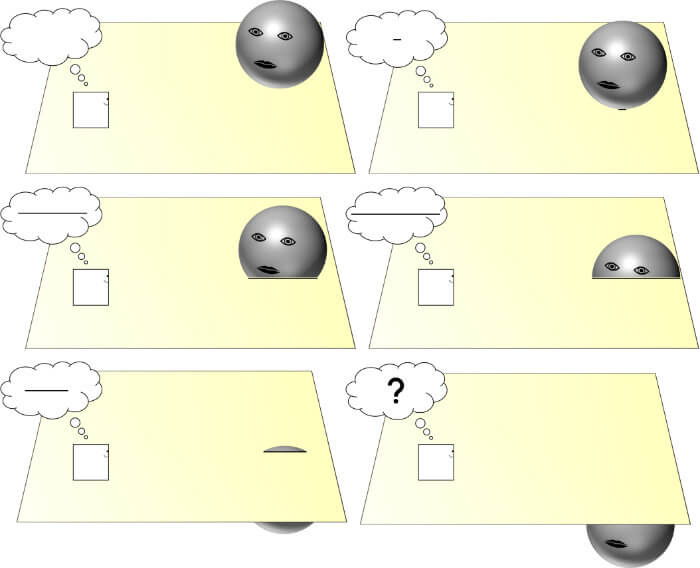
At this point, a Sphere enters Flatland announcing that he comes from three-dimensional Space. The Sphere tries to explain and prove the third dimension to A Square, 1) by describing the current location of individuals and objects in Flatland, 2) by moving in and out of Flatland, 3) by using analogies, 4) by picking up a tablet from a closed cupboard without opening the doors, and 5) by touching the side of A Square’s body (his inside) until he feels pain.
However, just as the King of Lineland could not understand A Square’s description of additional dimensions, so does A Square not comprehend Sphere’s description of a third dimension.
As a last resort, the Sphere propels A Square out of Flatland and into the third dimension. Now, navigating through Spaceland, A Square is in awe by what he can see: geometric figures instead of just lines, and the interior of every house, object and inhabitant. A Square thinks the Sphere to be a god, given his ability to see all things. However, the Sphere scornfully responds that, if that were the case, then all Spaceland criminals should also be worshiped, since they possess the same skill as the Sphere.
The Sphere then takes A Square to a meeting where the highest ranked Circles are passing a law that allows them to kill or imprison any shape that claims to have been visited by Spaceland inhabitants. When the Sphere intrudes into the meeting announcing he is from Spaceland, the Circles try, in vain, to arrest him, but the Sphere is able to simply move to the third dimension and escape.
All the policemen that witnessed the event are killed, and A Square’s brother, who was also present at the meeting, is imprisoned for life.

| | Point [0 dimensions] | Line [1 dimension] | Square [2 dimensions] | Cube [3 dimensions] | Tesseract [4 dimensions] |
|---|---|---|---|---|---|
| Vertices | 1 | 2 | 4 | 8 | 16 |
| Edges | 0 | 1 | 4 | 12 | 32 |
| Squares | 0 | 0 | 1 | 6 | 24 |
| Cubes | 0 | 0 | 0 | 1 | 8 |
| Tesseracts | 0 | 0 | 0 | 0 | 1 |
When A Square and the Sphere return to Spaceland, the Sphere explains the concept of solids, and even introduces him to a living Cube.
A Square then ponders that if the Sphere is able to see the insides of Flatlanders, perhaps a higher-dimensional creature than the Sphere exists who would be able to see the insides of the Sphere. He continues by theorizing a shape existing in four dimensions, which would be bounded by 8 cubes and 16 terminal points. A Square is describing a tesseract – a four-dimensional cube (see figure and table above).
The Sphere vehemently denies the existence of such a Space, although he later acknowledges hearing rumors of a fourth dimension, which he believes are simply the product of people’s imagination. A Square, now thoroughly ecstatic, postulate the existence of even higher-order dimensions – five, six, seven… – and expresses his wish to keep ascending the ladder of these extra dimensions.
Annoyed by all this talk, the Sphere finally pushes A Square back to Flatland.
After returning to Flatland, A Square dreams that the Sphere takes him to a zero-dimensional world called Pointland, which is inhabited by a single zero-dimensional point. When A Square tries to communicate with the Point and make him see the insignificance of his world, the Point assumes the voice is coming from his own rebellious mind.
The Point believes he is the entirety of the universe. The simple concept of plurality is unfathomable to him, since he has no awareness of length, width or height. All that exists is an infinitesimal small point.
The Sphere takes A Square back to Flatland, apologises for his previous outburst of anger and inspires him to preach the Gospel of the third dimension. Before the Sphere departs, he rewards A Square with images of what appears to be fourth-dimensional objects.
After waking up from the dream, A Square is decided to spread the word about the third dimension.

Hearing the proclamation from the Council to punish anyone who claims to have received revelations from another world, he decides to be cautious and share his knowledge with his bright grandson first. However, A Square is unable to demonstrate the concept of upward, due to the limitations of the two-dimensional Flatland, and the grandson dismisses him.
Disheartened by his inability to draw accurate and clear diagrams of three-dimensional objects, he eventually takes increasing risks by revealing his ideas of the third dimension in public, including a full account of his experiences in Spaceland during a meeting of the Local Speculative Society.
A Square is immediately arrested and sentenced to life imprisonment. Having failed to convert Flatlanders, he devotes himself to writing up a treatise about the mysteries of the third dimension, with the hopes that it may eventually help individuals to free themselves from a limited dimensionality.

In literature, a satire is the employment of humour with the aim to criticize and/or show faults or weaknesses of a particular idea, institution or individual.
Abbott lived in Victorian England, a period marked by social and cultural tensions and a stark division of classes. It is this class rigidity that Abbot is satirizing with his novella.

The autocratic government of Flatland means that Circles do not hesitate in applying their powers to keep the social order, while favouring the elite and harming the poorer and powerless classes.
The social hierarchy is so entrenched in the minds of Flatlanders that they appear complacent with the status quo. Saving sporadic rebellions (e.g., Color Revolt), the different classes simply accept the absurdity and cruelty with which the Circles manage Flatland, including strict regulation on the sciences, arts and business.
Something new that disrupts the social order is quickly suppressed.
Abbott is showing how a social hierarchy dominated by a strict class rigidity is pernicious to personal and social freedom. During his lifetime, Victorian Britain was organized in distinct social classes that have a striking resemblance to those in Flatland. In fact, the Victorian clergy had a similar prestige and influence in state decisions with regards to education, justice and politics.
The narrator of the story, A Square, is directly affected by limitations to freedom of speech. After learning that Flatland is all but a drop in a much bigger ocean, he sacrifices his relationship with his friends and family to devote himself to spreading true knowledge of the existence of a third dimension, knowing it would lead to his incarceration.

His quest seems commensurate with that of many scientists and classical philosophers in the past that put their careers and reputation in jeopardy for not conforming to established dogmas. The Victorian era was no exception. A good example is Charles Darwin who was ridiculed and defamed when he proposed his theory of Evolution by natural selection (see figure above).
A Square’s determination to preach the Gospel of the third dimension is moving, because, despite his righteous endeavours to enlighten people, his efforts were doomed to fail in a rigid society that strives only to maintain the social status quo for the benefit of the higher classes.

Flatland’s State appears to make use of certain “Laws of Nature” as means to cement distinctions between classes, and to prevent uprisings within the lower classes.
For example, in rare occasions, Isosceles triangles may produce a male child with equal sides (an equilateral triangle). The child is then taken from their parents and raised by a family of Equilateral as a certified Regular, never to hear from its biological parents ever again. Thus, by allowing Isosceles triangles to believe that ascending the social hierarchy is a possibility, they often renounce their potentiality to agitate the masses into rebellion.
Another “Law of Nature” states that physically irregularity amounts to moral irregularity. So, Irregular shapes with a critical error of angle deviation are immediately killed or destined to become criminals.
In addition, certain lower class Isosceles triangles are sometimes used as “specimens” in schools for instructional purposes. These individuals have no civil rights; they are abused and killed when their utility ceases, and then simply replaced by new “specimens”. This is genocide on a regular basis.
Perhaps Abbott is criticising the attitudes of Victorians towards people with special needs, who, for many Victorians, were considered lunatics and simpletons, locked up in asylums, with little chance to get employed or have an education. Or perhaps Abbott is drawing a parallel to the cruelties perpetrated by the British Empire to non-British and non-white individuals of its colonies.

In Victorian England, social norms dictated that women should be confined to domestic duties and motherhood. So, women would be expected to obey their husbands at all times, to provide them with a clean house and meals, and to take care of the children. A great deal of importance was also given to physical appearance and etiquette, and deviations from men’s ideal of femininity were highly discouraged.
Women couldn’t vote or open bank accounts, had no representation in government, were barred from doing similar work as men, and any cash or property they possessed belonged to their husbands. Even though some women could read, there was limit to how much knowledge they could gain. Engaging in political or scientific conversations, for example, was frowned upon. Education for women was, thus, strictly intended to make them more suitable companions for their husbands. These restrictions only helped to reinforce the myth that women had limited intellectual capacity and that reading a simple newspaper was too intense for their delicate minds.
The oppression of women in Flatland bears a striking resemblance to the situation of women in Victorian Britain. In Flatland, whereas men are full geometric figures, women are simple line segments with no chance of ever becoming polygons and rise to higher classes. They are considered inferior to men, lacking intelligence, sense of justice and rationality. Women are refused to a formal education and are only valuable as long as they have certain physical characteristics.

Interestingly though, Abbott assigns women way more power than they actually had in Victorian times.
In late 19th Britain, physical abuse towards wives was prevalent with very limited legal protection available to them. Men were also often adulterous with little to no consequence to their status, whereas if women committed adultery they would be disgraced.
Women could not divorce their husbands on the sole basis of infidelity either, so they mostly endured humiliation and their husbands’ constant cruelty. If they did file for divorce, they ran the risk of losing custody of their children and any possessions they might have acquired during marriage, potentially becoming ostracized and living impoverished lives.
In Flatland, however, women are actually a source of fear to men. Because of their sharp edges, they pose physical danger to their husbands if they happen to be positioned at a certain angle. Moreover, men often try to appease their wives whenever they get angry, because, due to their poor memory and fiery temper, they could easily kill their husbands and later have no recollection of it.
Perhaps Abbott gave Flatland women the power to induce fear in their husbands, so that the higher classes could use this to justify their discriminatory actions towards women. In other words, the state wants its inhabitants to believe that denying women basic rights is a necessity for the sake of the well-being of Flatland.
It somehow echoes the Victorian rhetoric that women should be confined to the domestic sphere and engage in men’s affairs, as giving women more “powers” could begin to disrupt a severely patriarchal society.
I bet Flatland will whet your appetite for learning about dimensionality.
Thinking about worlds with lower (or higher) dimensions than our own 3D world will, most likely, leave you perplexed, but Abbott’s charming drawings were a great didactic tool to understand the concept of dimensionality.
It was interesting the depiction of lower-dimensional objects as always being doubtful of the existence of a higher dimension, and attributing the feats of higher-dimensional individuals to treachery or even magic. The Point of Pointland (a zero-dimensional world) couldn’t conceive anything existing but his own self; the King of Lineland (a one-dimensional world) could not get to grips to A Square’s description of Flatland; A Square (living in 2-D Flatland) could not envision the 3-D world of Spaceland. The Sphere from Spaceland rejected the existence of a fourth dimension. No matter how hard they tried, their minds were simply ill-suited to imagine anything above the dimensions they existed in.
Apart from the treatment of spatial dimensions, Abbott likely wrote Flatland as a social satire, given that several elements of the story bear a striking resemblance to the Victorian society of his time: the stark class rigidity, the oppression of lower classes, the views on disability and the pervasive misogyny.
Sadly, Flatland lacks a gripping storyline. It’s didactic, it reads like a textbook, but Abbott’s convoluted explanations and regular digressions makes it a difficult and dry read at times. Ultimately, it fails to deliver enough entertainment for me to consider it a great novel.
But, who knows, maybe I’m being too one-dimensional! :p
I must admit that, being a father of two lovely daughters and married to a wonderful woman, reading Abbott’s descriptions of Flatland’s women made me extremely uncomfortable.
In fact, many readers have accused Abbott of being sexist and misogynistic, but that couldn’t be further from the truth. As I have now learned, not only was Abbott a fierce defender of women’s rights, but he was also one of the leaders of the Women’s Education Movement during his lifetime. He was also pivotal in creating educational opportunities for women through his correspondence with the Headmaster’s Conference and the Teacher’s Training Society, and was extremely critical of the general Victorian attitude towards women.
Flatland was a satirical response to the extremely unjust and abhorrent Victorian mentality towards women.
The old adage “don’t judge a book by its cover” couldn’t be more pertinent here.
See you in the next article!
Masterpiece
Mind-blowingly weird
c’est bien..
thanks..
Hi,
Thank you for your comment, and I’m glad you enjoyed the article 🙂