Introduction
If there is a subject I like to see depicted in entertainment and art, it is definitely mathematics.
I love maths – sometimes I spend hours on Khan Academy going through the math courses, and I have now countless books on the subject.
However, this wasn’t love at first sight…
In high-school I wasn’t particularly motivated to study maths, and, if I’m being honest, I kind of sucked at the subject.
I did however have a muse that got me, momentarily, interested in maths.
It wasn’t Rachel Riley, but someone just as interesting: Gyro Gearloose.
That’s true folks, my muse was an anthropomorphic chicken with a silly hat and a tiny robot with a light bulb head as an assistant.
For some reason, I warmed towards this character from Disney, and at some point, I decided I wanted to become an inventor.
Seeing Gyro surrounded by mathematical formulas, I realised I needed to seriously apply myself, and for a moment my grades did improve.
Unfortunately, Gyro wasn’t enough of a motivation to keep up. To my parents’ chagrin, I eventually gave up on the idea of becoming inventor and concentrated my efforts (again, short-term) to become a detective (and guess who my inspiration was?).
I had to wait for a few more years to truly understand the beauty of maths.
I’m no mathematician, but I surely envy their ability to look at nature and think in numbers. Isn’t it awesome that you can converse in a language that is made up of numbers?
Not only that, mathematics is the true language of the universe, in that if we ever encounter aliens, mathematics would certainly be the common language.
Indeed, the mind of a mathematician must really be a fascinating world.
And that brings me to Pi, the movie.
Review
The film stars Sean Gullete as an unemployed mathematician called Max, who appears to suffer from sporadic migraine headaches, paranoia and hallucinations.
Max believes that Mathematics is the language of nature – that is, every natural phenomenon (e.g., a volcano erupting, melting chocolate) can be represented through numbers.
Crucially, Max has convinced himself that there is an implicit pattern in the stock market – a kind of big number that represents the global economy.
He dutifully tries to figure out what that pattern is with the help of his computer, cutely named “Euclid”.
At one time, Euclid prints out a mysterious number, but thinking it had been a malfunction, Max immediately discards it.
Meanwhile, Max is recruited by agents from a Wall Street firm who show interest in his work.
He regularly visits his mentor, Sol Robeson, who had been looking for a pattern in \pi before a stroke put an end to his research career.
He also encounters a Jewish man, Lenny Meyer, who is doing mathematical research on the Torah and is searching for a pattern consisting of 216 digits long.
Eventually, Max realises that everything is connected via this mysterious 216-digit number, including the Torah and the stock market and Sol’s research on \pi .
The film progresses as Max gradually psychotic episodes intensify, slowly driving him to insanity.
The film was certainly entertaining and I sympathise with the premise that all natural phenomenon can be expressed by mathematical patterns.
I was already familiar with most of the mathematical concepts presented in the film, and appreciated that scientific rigor was not neglected.
Aronovsky appeared to have consulted with mathematicians, and all equations shown in the film are seemingly accurate. He and his team also did extensive research on migraines and on the stock market.
One criticism I have is that although the high-contrast black-and-white reversal film undoubtedly sets the underground feeling that Aronovsky surely intended, I found some scenes visually difficult to discern, which kind of ruined the experience at certain points.
In addition, even though the techno soundtrack really created the adequate vibe, I found that the sound mixing could have been better as I had to resort to subtitles at times to make any sense of the dialogues.
Our rating
As I mentioned above, I enjoyed the movie and the accuracy with which mathematical concepts were presented. There were a few minor points that I felt could have been improved, but given the limited budget available and unforeseen expense cuts that ensued, the production team is hardly to blame. Here, at Mindlybiz, Pi gets a star rating of 3.5.
Bizarrometer
Overall, the story line remains relatively easy to follow. However, the film contains a few unexplained and strange events, and the ending is somewhat ambiguous. For that reason, Pi gets a Bizarrometer score of 3.
Pi (briefly) Explained!
You don’t need a lot of imagination to figure out that a film called Pi with the number \pi on the promotional poster has probably something to do with the mathematical constant \pi (if you don’t know what that is, keep reading below).
But you would be wrong to assume that it is only about this number. The themes incorporated in the film vary far and wide, and this article will only skim through some of them.
At face value, the film appears to promise the ultimate human quest: understanding the essence of everything around us.
Max, the main character of the film, is convinced that everything, including people, exists in a state of disorder. However, within this disorder, there is a pattern, a natural order within it. If you understand that pattern, you understand the meaning, or essence, of whatever thing you are trying to manipulate.
Max’s theory reminds me of the alchemical idea that we explained in a previous article: every substance (be it a rock, an ant, or a human mind) consists of a corrupted (disordered) First Matter that needs to go through several purification stages (brought into a state of order).
The similarities don’t end here. According to alchemists, the First Matter is the same in every substance, only organised differently – similar to Max’s belief that every natural phenomenon can be explained by a mathematical pattern.
In the film, the pattern is hidden within a number consisting of 216 digits, and it represents the one fundamental Truth. You can go as far as to suggest that knowing this pattern will make you omniscient (knowing everything) and perhaps even omnipotent (able to do anything).
For example, as Max states: “Even if we are not sophisticated to be aware of it, there is a pattern, an order, underlying every GO game. Maybe that pattern is like the pattern in the stock market. The Torah. This 216 number.”
This is also suggested by Sol’s research, through which he realised that computers appear to become conscious after spitting out the 216-digit number. In Max’s words: “Studying the pattern made Euclid conscious of itself. It died spitting out the number. Consciousness is the number”.
So, decoding the pattern within this 216-digit number would not only give you the ability to understand nature but also to create life – if you define life as the state of being conscious of course.
But I believe the film alludes to a more sobering reality.
Max’s endeavour to unravel the essence of all things using mathematics turned out catastrophic, slowly driving Max to insanity.
If there were indeed a mathematical pattern underlying all natural phenomena, then it’s likely that we humans would never be able to crack it.
Now, what does this actually have to do with \pi , the number?
As I’ll explain later on, I believe Aronofsky got his inspiration for the storyline from some of the most peculiar properties of the number \pi .
But before we dig into the most meaningful events in the film, let me share with you some interesting facts about the number \pi .
Seven cool facts about \pi
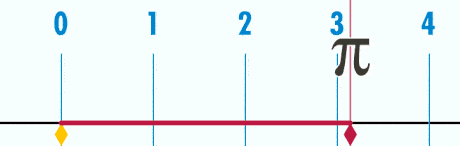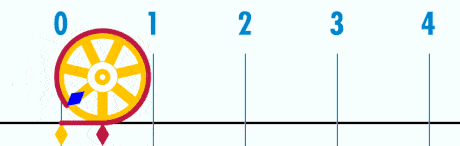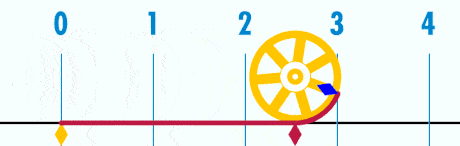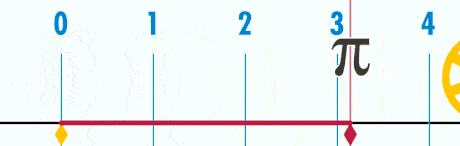
1. \pi is always equal to the ratio between the circumference of a circle and its diameter
Think about it this way: Imagine a spaghetti string that you join at both tips to form a circle.
Now, with a ruler, measure the length of the spaghetti circle from one side to the other, making sure the ruler passes by the center of the circle – this is the diameter of the circle (let’s say it’s 7 cm).
Next, measure how long the spaghetti string is – this is the circumference of the circle (let’s say it is 22 cm).
If you divide the circumference by the diameter, you get 3.142857…
Well done, you’ve just calculated \pi ! Well, a rounded up version of it.
Another way to think about it is like this: if you divided the spaghetti string into equal parts, each single part would equal exactly \pi !
Now, the size of the circle doesn’t really matter – by taking the ratio of the circumference to its diameter you will always get \pi .
That means that if you take a circle the size of a pea and measure the ratio of its circumference to its diameter, you will get \pi .
If you take a circle the size of the Earth and measure the ratio of its circumference to its diameter, you will also get \pi .
In fact, take any circle you can think of – a circle the size of the universe for example – measure the ratio of its circumference to its diameter and you are guaranteed to get \pi .
And note, you are not getting an approximation of \pi . If you had access to an absolutely precise measurement tool, you would get the full-blown \pi with all its inherent oddities (keep on reading to find out which ones).
Isn’t that truly mind-blowing?
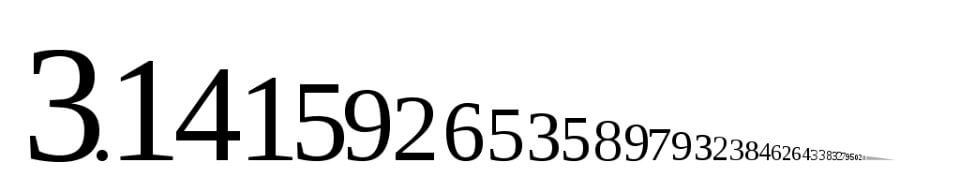
2. \pi has an infinite number of decimal digits
\pi is an irrational number, which means that it cannot be written as a fraction between two integers.
A fraction is a number like ½, or -17/32, where the top number is a numerator and the bottom number is the denominator.
For example, 4 can be written as the fraction 8/2. Even a number with an infinite number of decimal places such as 1.3333… (the dots mean that it goes on infinitely) can be represented by the fraction 1/3.
Another example is 1.571428571428571428 571428… . It has an infinite number of decimal places, but it can still be represented by the fraction 11/7. If you look closely the sequence 571428 repeats over and over again.
What about \pi ? It turns out that there aren’t two integers that can make up this number.
Approximations do exist of course: For example, 22/7, but if you looked far enough you would see the same sequence of numbers repeating.
In contrast, the digits of \pi go on forever in a seemingly random fashion.
As of 2021, the record holder for calculating the longest string of PI digits belongs to Timothy Mullican, who managed to calculate a whopping 50 trillion digits using a computer programme called y-cruncher.
3. \pi is a transcendental number
Now, \pi belongs to a more special category of numbers called “transcendental numbers”.
I covered transcendental numbers in another article describing the squaring the circle problem, so be sure to read that as well.
In short, being transcendental means that the number is not the solution to any polynomial equation of the kind 2x = 1 (numbers that are solutions to polynomial equations are called algebraic numbers; see What is algebra?).
According to Wikipedia Algebra means “reunion of broken parts”. So, in a sense, it means taking something that is incomplete and make it complete.
Take this polynomial equation: x + 1 = 4
The goal of algebra is to figure out what the unknown variables in equations are (like the variable x above). You have something you don’t know (variable x ) and you use Algebra to figure out what it is (in the example above x is equal to 3, because 3 + 1 = 4). In Algebra you always need to keep one side of the equation equal to the other.
Algebra is very important in real life for describing and modelling things in the real world (like predicting whether an asteroid is likely to crash on Earth).
Algebraic numbers are numbers that cause a polynomial expression to equal 0.
Let’s say you have a number like 0.25. 0.25 is the solution (also called root) of an equation such as 100x – 25 = 0 . Why? Because if you solve the equation for x :
1) 100x = 25
2) x = 25/100
3) x = 0.25
So 0.25 can be expressed in terms of an equation; that is, 0.25 is a solution (or root) to the equation 100x – 25 = 0 .
Therefore 0.25 is said to be an algebraic number, because it causes a polynomial expression (the 100x – 25 bit) to equal 0.
You can pretty much come up with any number and you’ll see that it is always a solution to a polynomial expression.
Always? Well, no, not always.
It turns out that \pi is not the solution to any polynomial with integer coefficients.
It doesn’t matter if the equation is 1 +x = 1213x^2 + 48x -4 , or whatever freaky equation you might conceive. There is simply no equation with integer coefficients in which x will equal \pi .
A mathematician called Ferdinand von Lindemann proved that \pi is not a constructible number, and if \pi is not a constructible number, it cannot be algebraic.
Mathematicians baptised non-algebraic numbers with the name “transcendental” because, according to a famous mathematician called Euler, “they transcend the power of algebraic methods”.
Contructible numbers are numbers that can be constructed with a compass and straightedge in a finite number of steps. 10, 1302, \sqrt{2} are all constructible numbers.
Algebraic numbers contain all constructible numbers plus a few more. You can construct \sqrt{2} using a compass and straighedge, but you cannot construct \sqrt[3]{2} (cubic root of 2). So anything higher than a square root ( \sqrt[3]{2}, \sqrt[4]{2}, \sqrt[5]{2} and so on) are algebraic (but not constructible numbers).
Both algebraic and constructible numbers are solutions to algebraic equations (check out What is Algebra?).
Transcedental numbers are numbers which are not solutions to any algebraic equation. Some examples of transcendental numbers are \pi, e and \ln 2 .
Here’s some food for thought:
On the one side, we have a bunch of numbers that are familiar to us and which we know how to “create” and manipulate (i.e., algebraic numbers). These numbers make up most of the numbers we, non-mathematicians, will ever have to deal with in life.
On the other side, there are these obscure numbers which are used to compute all sort of things (for example, area of circles) with very high precision, but of which we have no fricking clue how to construct them.
Keep this thought in mind, because it’s relevant to the analysis of the film!
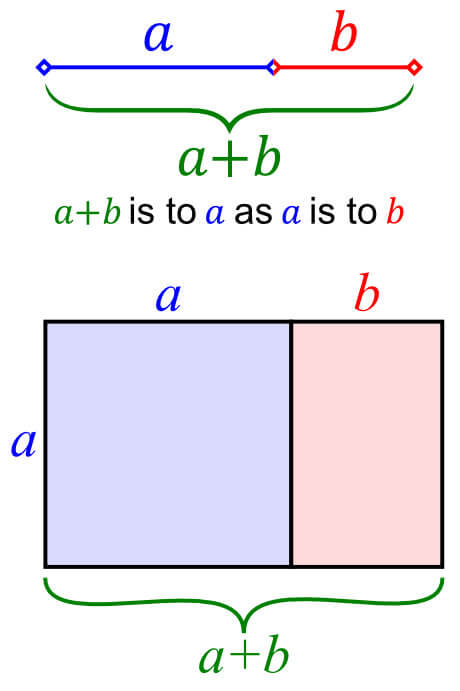
4. \pi is related to the golden ratio in numerous ways
The Golden Ratio (also denoted by the greek letter phi: \phi ) is another irrational (but not transcendental) number.
I ask you now, why?
If you read the previous facts above attentively, your answer should be “because, although it cannot be written as a fraction between two integers (therefore, irrational), it is a solution to an algebraic equation (therefore, not transcendental)”.
And you would be correct!
The golden ratio starts with 1.6180339887 … and goes on infinitely. It is the solution to the polynomial equation x^2−x−1=0 , which is why it is not a transcendental number.
Just as \pi is the ratio between the circumference to its diameter, the golden ratio is also a ratio. To better explain what that ratio is, look at the left figure above. If the ratio of a+b to a is the same as the ratio of a to b, then the two line segments are in the golden ratio.
Similarly, if the ratio of the longer side of the pink rectangle (i.e., a) to the shorter side of the pink rectangle (i.e., b) is the same as the ratio of the longer side a+b to the shorter side a, then you have a golden rectangle.
Interestingly, there are many ways in which \pi and the golden ratio are related, although a fairly good level of math skills are required to really understand how.
The point of the paper I linked above is that \phi (the golden ratio) is the smallest of the Golden Numbers whereas \pi is related to the largest one.
There are other geometrical and numerical relationships between the two numbers, meaning that the golden ratio is associated with \pi in meaningful ways, such that you could theoretically get from one number to the other.
Mathematicians have been discovering interesting avenues in which \pi and the golden ratio are related and they believe that this relationship might be even greater than currently thought.
5. \pi is very likely a normal number (but not yet proven)
\pi has an infinite number of decimal places, right? Does that mean it would theoretically be possible to find any imaginable sequence of numbers?
For example, let’s say you wished to determine if the sequence 999999 existed within the decimal digits of \pi .
Indeed, you would be able to find this sequence in the decimal place 762.
Here are the first 1000 digits of \pi :
3.14159265358979323846264338327950288419716939937510
58209749445923078164062862089986280348253421170679
82148086513282306647093844609550582231725359408128
48111745028410270193852110555964462294895493038196
44288109756659334461284756482337867831652712019091
45648566923460348610454326648213393607260249141273
72458700660631558817488152092096282925409171536436
78925903600113305305488204665213841469519415116094
33057270365759591953092186117381932611793105118548
07446237996274956735188575272489122793818301194912
98336733624406566430860213949463952247371907021798
60943702770539217176293176752384674818467669405132
00056812714526356082778577134275778960917363717872
14684409012249534301465495853710507922796892589235
42019956112129021960864034418159813629774771309960
51870721134999999837297804995105973173281609631859
50244594553469083026425223082533446850352619311881
71010003137838752886587533208381420617177669147303
59825349042875546873115956286388235378759375195778
18577805321712268066130019278766111959092164201989
But let’s try more exciting sequences.
For example, let’s say you want to find the sequence 0123456789 somewhere within the decimal expansion of \pi .
Now, if you look at the first 100 decimals, will you find this sequence? Clearly no.
What if you look within the first 1000 decimals? Also no.
Ok, what about 10000? No.
Well, surely in 1000000 (that’s one million numbers)? The answer is still a resounding No!
In fact, you would need to go to the 17.387.594.880th decimal place (that’s more than seventeen billion digits!) to arrive at the 0123456789 sequence.
There are even online tools that help you find sequences within \pi . For example, mypiday is a popular tool to find out where in the number \pi you birthday date (or any other date for that matter) is located.
This surely begs the question: can we make the point that any combination of numbers that you can think of will be represented somewhere in \pi ?
In order for that to be the case we would need to demonstrate that \pi is a normal number.
In mathematics, a number is considered normal in the base-10 number system (i.e., numbers with digits that consist of integer values ranging from 0 to 9) if, across its decimal development, there is an equal frequency of the integers 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
Although, it has not yet been proven that \pi is a normal number, mathematicians suspect that it is.
Consider the table below, which contains the number of times that each number from 0 to 9 shows up within the first billion decimal digits of \pi :
| Decimal digit | Number of times the digit appears |
|---|---|
| 0 | 99.999.485.134 |
| 1 | 99.999.945.664 |
| 2 | 100.000.480.057 |
| 3 | 99.999.787.805 |
| 4 | 100.000.357.857 |
| 5 | 99.999.671.008 |
| 6 | 99.999.807.503 |
| 7 | 99.999.818.723 |
| 8 | 100.000.791.469 |
| 9 | 99.999.854.780 |
| Total | 1.000.000.000.000 |
Sure, there are visible differences in the frequency with which each number appears. However, it’s not a stretch to imagine that as mathematicians keep on discovering more and more \pi digits, the differences between frequencies will diminish and, who knows, maybe even equalise.
6. \pi is present in statistics
This is my personal favourite. You might think that \pi , being a number with such odd properties and which is mostly associated with circles, cannot be possibly involved in probability and statistics.
However, it is.
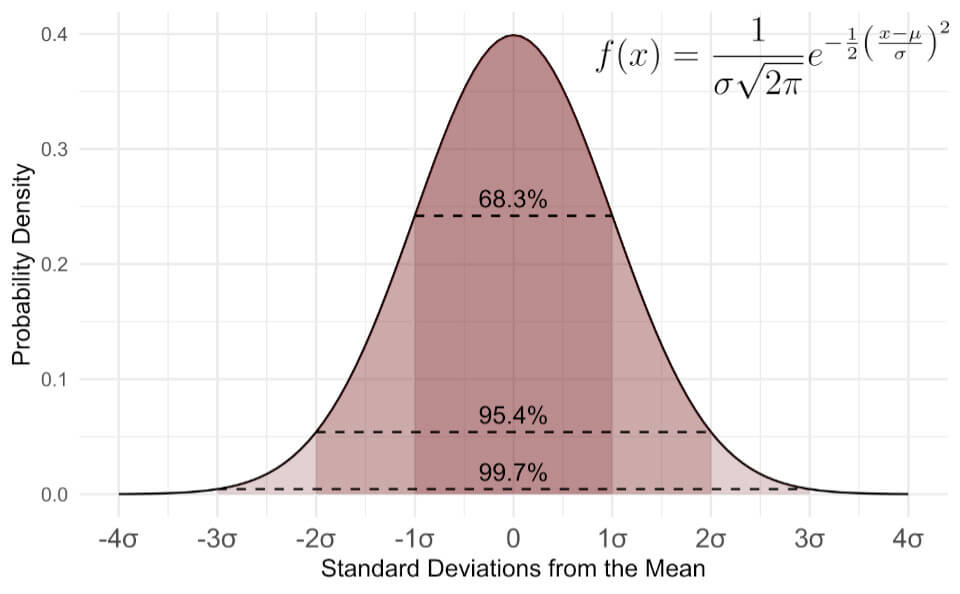
For example, \pi appears in the normal distribution formula, the most common distribution used in statistics.
The standard normal distribution is a probability distribution formed by continuous variables (things that are measured and can take on an infinite number of values between any two values).
Here’s how it works. Imagine that, for some reason, you wished to know the height of people in New York.
You cannot measure the height of every single person, so you need to select a representative sample.
So, you go out to a busy street in New York and start measuring the height of people you select at random. Let’s say you measure the height of 100 people.
Some people will be tall, some short, but you will be able to calculate an average from those 100 people (say it’s 1.86 m).
However, it could happen that this particular street is frequented mostly by basketball players, so the height you measured might not be very representative of the whole population of New York.
So, you go out to another busy street in New York and measure the height of another 100 people and take the average of all those heights (e.g., 1.70 m). Let’s do this in 1000 streets, each time picking 100 people at random.
Now, if you plot all those 1000 averages (1.86, 1.70, etc), you will get something like a normal distribution plot with its distinctive bell-shape curve (watch this video for a visual explanation of the concept of standard normal distribution). It turns out that many variables are normally distributed if you plot the averages of selected samples as I did with height (e.g., weight, throw of dice, IQ, stock volatility, length of leaves, etc.).
But what does that have to do with \pi ? After all, isn’t \pi all about circles? What does the standard normal distribution have to do with circles?
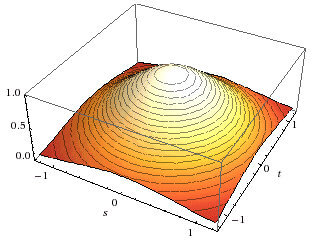
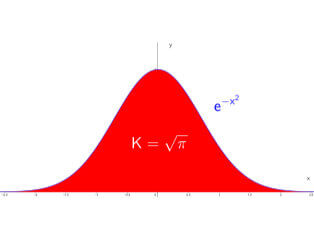
It may not be obvious, but the standard normal distribution is indeed related to circles.
When you square the probability function you go one dimension up. If you look at the 3d plot of the distribution and look at the contour lines you will the circles.
Also, when you center and standardise the curve, such that the mean is zero ( \mu = 0 ) and the variance is one ( \sigma = 1 ), the area under the curve is equal to \sqrt{\pi} .
There are many more situations in statistics in which \pi will be involved, such as the probability of two randomly chosen integers being prime numbers between them (which is equal to 6/\pi^2 ), Buffon’s needle problem, tracking population dynamics, etc.
7. \pi is just one among an infinite number of transcendental numbers
Now that I have hopefully awed you with some fascinating facts about \pi , you might think that \pi is a truly unique number, perhaps even magical.
Well, it is not.
It turns out that the number \pi is not really that special. It’s now a mathematical truth that there are way more transcendental numbers than there are algebraic numbers!
If this hasn’t really sunk in, I’ll rephrase it: there are more transcendental numbers (numbers that are so weird that defy our understanding) than numbers we use in our daily lives.
Another way to think about it is to consider the numbers you are familiar with.
So think about the amount of numbers you can imagine: start with 0 and continue with 1, 2, 3, 4, … 100, …, 1000000 and so on until infinity. Well, what I’m saying here is that there are more transcendental numbers than all of those you can count!
For those perspicacious among you, you may have noticed that I wrote that you should count numbers from 0 until infinity.
I then went on saying that there are way more transcendental numbers than those.
But wait a minute! How can there be more transcendental numbers than infinity itself?!
Welcome! You have just entered a truly bizarre corner of mathematics.
First, let’s play a fun game. Let’s say you have one bag containing an infinite number of M&M’s, and you take them out, one by one (no matter how many you take, there’s always one more in the bag).
OK, so let’s count the number of M&M’s that come out of that bag – these are your natural numbers:
Natural numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 … \infty
Now, I would like to ask you to think of the even numbers only.
Even numbers: 0, 2, 4, 6, 8, 10 … \infty
My question to you is this: which set do you think is larger: the set of natural numbers or the set of even numbers?
If your answer was “well, obviously there are more natural numbers since they include all even numbers plus all the odd numbers”, you are not alone (I myself once thought that).
However, you are wrong!
It turns out that there are an equal amount of infinite numbers in both sets.
And this is why: If you always multiply each natural number by 2, you will always be able to match it to an even number:
| Natural numbers | 1 | 2 | 3 | 4 | 5 | ∞ |
| Even numbers | 2 (1 x 2) | 4 (2 x 2) | 6 (3 x 2) | 8 (4 x 2) | 10 (5 x 2) | ∞ |
Even if you pick the 10000th M&M you can always match it with 2 x 10000.
If you pick 122.039.482.948.280th M&M you can match it with 2 x 122.039.482.948.280.
It doesn’t matter how many M&M’s you pick, you can always find a match by multiplying a number by 2.
In a moment of sheer brilliance, Georg Cantor even proved that rational and even algebraic numbers are also enumerable. That is, you can always match them one-to-one with natural numbers (watch this easy-to-follow demonstration of how the rational and natural number sets are matched in size).
But what about transcendental numbers? Can they be matched to an infinity set of natural numbers just like the even numbers or the rational numbers?
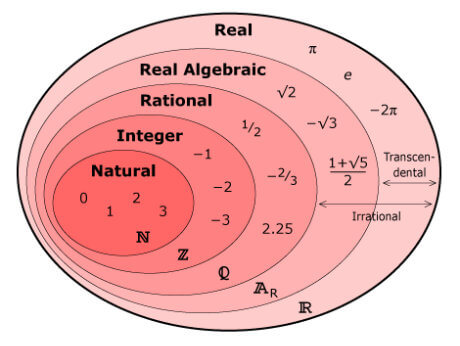
It turns out they cannot! To understand why, let’s keep it simple and only consider a list of real numbers, \mathbb{R} (the number set which contain transcendental numbers; see the diagram on the right figure above), that exist between 0 and 1:
| Natural Number | Real Number |
| 0 | 0.194728… |
| 1 | 0.857772… |
| 2 | 0.943289… |
| 3 | 0.409839… |
| 4 | 0.998378… |
| 5 | 0.382922… |
Remember, this is important – you have to think that this list goes on forever, such that you list all real numbers.
Now, you might wonder why can’t we just assign 1 to the first element, 2 to the second, 3 to the third and so on, just like we did when we matched the natural with the even numbers.
To show you why this doesn’t work for the real numbers, let’s take the first element of the first number, the second element of the second number and so on.
Your number will be 0.153872….
Now, let’s add 1 to each digit in your number and the result will be 0.264983….
Is this number on your list? You guessed it, it isn’t.
You can go ahead and add the number to the list if you liked, but that won’t matter. I can do this game over and over again with the numbers you add to the list.
In fact, there would be an infinite amount of numbers missing! I can come up with infinite ways to make a number that isn’t on your list – I added 1 in the example above, but I can also add 2, subtract 8.2, multiply by 0.1938164, and so on and so on – it will never ever stop.
Now, what is the implication of this? The implication is that there are way, way, way more numbers that lie between 0 and 1 than there are natural numbers (1,2,3,4, … infinity)!
As opposed to algebraic numbers, which comprise a countable infinite set (you can match them one-to-one to natural numbers), transcendental numbers comprise an uncountable infinite set (there are too many of them to be able to match them one-on-one to natural numbers).
In fact, consider this: if you were to pick a number randomly from all real numbers, the probability that you picked a transcendental number would be 1! That’s it: 1! That means you are guaranteed to pick a transcendental number – that’s just how many there are!
I find this utterly mind-boggling, because mathematicians actually only know a handful transcendental numbers (see the current full list of numbers that have been proven to be transcendental).
However, it has been proven that they amount to a much, much, much larger quantity than algebraic numbers.
Pi Explained!
So now we have some tools that will help us properly analyse the movie Pi.
In his quest to predict the stock market using his computer Euclid, Max stumbles across this number:
94143243431512659321054872390486828512913474876027671959234602385829583047250165232525929692572765536436346272718401201264314754632945012784726484107562234789626728592858295347502772262646456217613984829519475412398501
Throughout the movie, we are led to believe that this number contains the key to unlock the secrets of the natural chaotic systems.
Max says: “Even if we are not sophisticated to be aware of it, there is a pattern, an order, underlying every GO game. Maybe that pattern is like the pattern in the stock market. The Torah. This 216 number.”
Specifically, the number is significant in at least three different ways:
1) The Wall Street agents believe this pattern will unlock the secrets of the stock market.
The agents are working for a predictive strategy firm. They show an interest in Max’s research and convinced him to share his results by providing him with classified computer chip. Max is very evasive but somehow the agents manage to get their hands on one discarded printout that has only part of the number that Euclid spat out. Thinking they have the full pattern, the firm attempts to manipulate the stock market, only to see it crash. Enraged, the agents kidnap Max and demand that he discloses the rest of the code, at which moment he is rescued by Lenny.
2) The Jews believe the number is the key to unlock the true name of God.
Lenny Meyer, whom Max encounters at the café, believes the Torah is just a long string of numbers, a code that was sent to Jews from God. He and his fellow sect members are searching for a pattern in the Torah, which they know is 216-digits long. The leader of the sect explains that according to the Talmud, there was a temple that housed the Ark of the Tabernacle, which contained the 10 Commandments. In this temple, the High Priest would intone one single word: the name of God. The name of God, according to their tradition, was 216 letters long – as many letters as the number computed by Euclid. The Jews believe the 216-digit is the key that unlocks the door to the “Gardens of Eden” and meet God.
3) Sol believes that the number represents the consciousness of the computer.
While Sol was conducting his research on PI he came to the conclusion that certain problems cause computers to occasionally get stuck in a loop, and subsequently crash as a result. A few moments before the meltdown, however, these computers appear to become conscious of their own structure – they become aware that they are made of silicon and other materials.
Now, here’s a crucial point. The number that Euclid displays on the monitor isn’t the 216-digit number everyone is looking for. In fact, the number doesn’t even have 216 digits! It has 218 – go ahead and verify yourself if you like.
I have seen reviews and posts suggesting this might have been a blunder. Honestly, I am very convinced it wasn’t. Here’s why:
1) Aronovsky was careful to describe and display mathematical formulas and ideas very accurately. It’s hard to believe that the production team would have placed so much effort ensuring these mathematical ideas are accurate, but then not have bothered counting the number of digits of a number that is at the epicenter of the story.
2) We never, ever, actually hear Max saying that Euclid’s number is the much sought-after 216-digit number. Viewers are led to believe that it is, but Max never explicitly says it (or anyone for that matter).
3) When Max manages to compute the number a second time (after the trip to Coney Island), he starts writing it down on a sheet of paper. However, after a few digits he comes to a halt as if Euclid’s number has lost its importance. Max realises that the actual 216-digit number is already in his head. Indeed, a few moments later, he is seen attempting to find patterns on a completely different number scribbled on a newspaper page. And guess what, the number on the newspaper is exactly 216 digits! So the number shown on Euclid’s monitor is likely a set of instructions, a kind of recipe, on how to get the actual 216-digit number.
So why the discrepancy? What is the significance of the 218-digit number? What is the relationship to the actual 216-digit number?
The 218-digit number
Let’s begin with the 218-digit number computed by Euclid. Pay close attention to the digits the camera zooms in shortly before Max passes out (highlighted in red):
94143243431512659321054872390486828512913474876027671959234602385829583047250165232525929692572765536436346272718401201264314754632945012784726484107562234789626728592858295347502772262646456217613984829519475412398501
314 or, if you like, 3.14 – the first 3 digits of \pi . I don’t know if this is a coincidence or not, but the fact that 314 is not the center of the 218-digit number (or even the center of the particular row) makes me wonder why the focus on these particular digits.
It could be that Aronovsky is giving us a subtle clue that suggests this 218-digit number is actually part of \pi .
Remember fact number 5 If \pi is a normal number, then it’s certain that somewhere within its decimal expansion you will find the 218 sequence shown in the film. Although mathematicians aren’t sure if \pi is normal, they have a strong suspicion that it is.
At the beginning of the film, Max mentions that Sol stopped caring when he was so close to seeing the true nature of \pi . This suggests that the crux of Sol’s research was writing algorithms that recognise patterns in \pi .
Sol was searching for a pattern within \pi , but a stroke put a definite end to his working days as a mathematician.
The 216-digit number
\pi is a transcendental number, it transcends the algebraic tools we have to build numbers (see fact number 3).
As I mentioned above however, maybe there is a pattern underlying this number – a pattern that would finally allow us to understand chaotic structure of \pi .
This is related to the notion that whenever there is a chaotic system, there must be a natural order within its apparent randomness.
In fact, the reason of Sol’s stroke was likely linked to the discovery of the same 218-digit number that Max has found. But why did Max succeeded where Sol failed? One clue is given by the number written at Sol’s apartment after he suffered the fatal stroke. This is the number:
94143243431512659321054872390486828512913474876027671959234603285829583047250165232525929692572765536436346272718401201264314754632945012784726484107562234789626728592858295347502772262646456217613984829519475412398501
At first sight, the number appears to be identical to the one Euclid spat out. However, a closer inspection reveals a difference in two single digits that I highlighted in blue above (compare the two sequences above).
Sol was indeed close, but never really there. Was this a production error? Or did Aronovsky and his team purposely change the two digits in Sol’s note? If the latter, this could mean that attempting to manipulate the wrong 218-digit number could have contributed to Sol’s passing.
Remember fact number 2, all transcendental numbers are irrational, which means that there is no apparent pattern in their never-ending decimal representation.
However, what if encoded in \pi existed a set of instructions that would allow us to understand all transcendental numbers (those ones that transcend the mathematical tools we have for building numbers)?
This would be big in the mathematical community. The ability to “create” transcendental numbers would likely give us the tools to manipulate nature itself – Max’s ultimate quest.
This is the significance of the 218-digit number. It contains the set of instructions on how to generate the key to deciphering chaotic systems. And everything appears to point that the 216-digit number is the key.
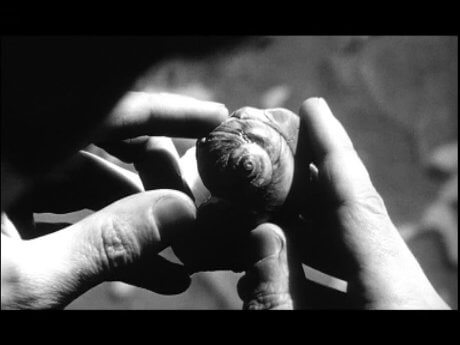
Remember the scene when Max takes a trip to Coney Island, where he notices a few shells with spirals on them on the beach.
This is an epiphany moment for Max. He realises the spirals could represent a way into finding out the secrets of that pattern.
He notices spirals everywhere: in his coffee, in shells, and perhaps more importantly, in the slimy substance that his computer, Euclid, produced before crashing (you can see the spirals when Max looks at the substance via his microscope).
Spirals can be described with the golden ratio, \phi . If you have two lines (one long and one short), and the ratio of the whole line to the longer line is equal to the ratio of the longer line to the shorter line, then the two lines are in the golden ratio (see fact number 4).
\pi is transcendental and so it transcends the algebraic tools we have to build it. But the golden ratio is not transcendental.
The golden ratio, even though irrational (i.e., has an infinite amount of decimal digits), it is an algebraic number (i.e., a solution to a quadratic equation; see What is algebra?).
Given it’s relationship with \pi , Max could have found a way to unlock the secrets of the number by using the golden ratio as a mediator in the understanding of transcendental numbers such as \pi .
He went back to his research and wrote an algorithm based on the structure of the spiral, which he knows is inscribed everywhere in nature.
When Max has this epiphany, a series of equations are shown, and guess what, the equations contain the number \pi .
Once again, this is related to fact number 4 that \pi and the golden ratio are related in meaningful ways, and possibly the solution to unravel the mysteries of \pi .
Interestingly, when he runs the algorithm via Euclid, it successfully prints out the 218-digit number it had printed out before.
However, as soon as Max begins to write it down, he halts. Why does he stop? Because he has figured out that the 216-digit number is in his head already – it isn’t the number Euclid is displaying on the screen.
In fact, a few moments later, we see Max trying out different combination of patterns on a completely different number written down on a newspaper page. This number has exactly 216 digits.
In fact, after Max discovers this 216-digit number he has yet another epiphany just as he is about about to kill the ant in his apartment.
He starts reciting some numbers (19 ½, 39 1/8, 6 ¾, 7 & 8, 12 ¼) and says “I know these numbers. They are going down, down, down…”. His mind is getting closer to the truth.
Then he meets with Sol, who immediately realises that Max has figured it out (this is also suggested by Darren Aronovsky himself in the director’s commentary of the film, where he says that in this scene Max “realises he is no longer searching, he has arrived”).
Max found the pattern! That pattern that connects all things in nature. And the pattern is not the actual 216-digit number he had found, but it lies inside his head.
It’s just a number
Doesn’t it seem odd to you that nobody has ever come across this number before?
I mean, with the manpower and resources of the Wall Street firm wouldn’t they be able to eventually stumble upon this number? After all, they are the ones providing Max with cutting-edge computer chips.
In fact, Max questions the Jews in this exact same point: surely, they must have written down every combination of digits, translated and intoned them all (well, actually they couldn’t have, see “Would it really be doable to compute every single combination of 216 digits?“).
No, not really, unless you have eternity on your side.
To get all possible combinations of 216 digits, you need 10^{216} (that’s 10 followed by 216 zeros!) combinations: starting with 0000… (216 zeros) until 9999… (216 nines), with all possible combinations in between.
Even if you had a computer that only took one millisecond to verify whether the number sequence is the correct one, you would need 3.17 \times 10^{204} centuries to go through them all.
To put things in perspective, the age of the universe is “only” 1.3 \times 10^8 centuries old.
So, as Max tells the sect leader, perhaps the number is really just a number. What matters is the syntax – the set of rules that lead to that particular arrangement of digits.
The conversation with the Jewish sect is very revealing. Max is convinced that while decoding the pattern he actually saw God.
When he’s trying to figure out the syntax of the 216-digit he’d written on a newspaper page, you can see part of a sentence “(Only God is P…” .
We cannot make out the rest of the sentence, but in the director’s commentary, Aronovsky mentions that it says “Only God is Perfect” and that this newspaper is hidden in other parts of the film.
So it is interesting this connection between the 216-digit number and God.
When he said he might have seen God, he could be referring to the moment when he realised the actual 216-digit long number is already in his head. Remember when he started writing down the number Euclid computed, but then stopped after joting down a few digits?
Shortly after realising the number was in is head, he has a terrible headache and the white void appears. This white void is also present just before the drill scene, where Max is standing in a completely white room in apparent tranquility, reciting seemingly random numbers.
Aronofsky mentioned in the director’s commentary that Sean (the actor portraying Max) should have done this scene completely naked. They decided against it, however, because Aronovsky thought it might be too distracting.
Still, the fact that Max should have appeared naked in this scene (perhaps as a parallel to how God created an also naked Adam) could represent Max’s purity of mind.
Could the white void represent the transition to enlightenment? The purity of mind he so long aimed to find?
If it does, it is obvious that Max now understands that this quest is ultimately destroying him.
He gets rid of the evidence by destroying his research tools and burning Sol’s research notes, and engages in trepanation to remove what he believes to be the source of his knowledge and pain – the vein above his right ear.
Conclusion
It is natural that humans attempt to understand the world around them: generations of thinkers and scientists have done so. Max, however, takes this quest to the limit, as he believes that there is an implicit pattern in everything in nature. Everything is therefore connected via this pattern: an organism of sorts, represented by a 216-digit number.
As Max gets closer to this fundamental Truth, his mental health deteriorates to the point that he begins to conflate reality with fantasy.
The film leaves us with the ambiguity of whether Max did in fact decode the pattern. Because the main character, Max Cohen, appears to suffer from Psychosis, it is unclear what/who is real and what/who is simply a figment of his imagination.
Perhaps he did, but feels that he cannot bear such responsibility and knowledge. Perhaps he did not, and the drilling was the act of a desperate man that recognised the limitations of the human mind. I guess we will never know.
Max’s final drastic behaviour is perhaps a reflection of the sobering reality that the human mind is simply not equipped to deal with this kind of knowledge. Perhaps it is better to be incognizant of the true meaning of life, and simply take joy in watching the leaves of a tree being blown by the wind.
Final thoughts
Mathematicians have proven that transcendental numbers (to which \pi belongs) are more numerous than numbers we are familiar with (see fact number 7). In a way then, \pi isn’t particularly special or unique. Claiming that \pi contains within it the pattern that explains every natural phenomenon, would be like saying that the genome of a cat contains everything necessary to understand all living organisms.
Perhaps this is true to a certain extent. Genetic differences between the cat and human species naturally vary, but you would be surprised to know that we share about 90% of the genes with the domestic cat.
So, perhaps the focus on \pi is meant to represent that crucial anchor to which all numbers are linked to. Maybe there exists a certain interconnection between all transcendental numbers that mathematicians have yet to discover. Think of how the 100 billion neurons are interconnected to support most of the operations of the brain, or how dark matter connect the two trillion galaxies across the entire universe in a gargantuan galactic dance.
I’m digressing, I know, but it is surely fun to speculate! 😉
See you in the next article!