This post is part of a larger deep dive
Curious about the role of the number pi in Pi? Check out Pi Explained!
Or read the full Pi article!
This post is part of a larger deep dive
Curious about the role of the number pi in Pi? Check out Pi Explained!
Or read the full Pi article!
So now we have some tools that will help us properly analyse the movie Pi.
In his quest to predict the stock market using his computer Euclid, Max stumbles across this number:
94143243431512659321054872390486828512913474876027671959234602385829583047250165232525929692572765536436346272718401201264314754632945012784726484107562234789626728592858295347502772262646456217613984829519475412398501
Throughout the movie, we are led to believe that this number contains the key to unlock the secrets of the natural chaotic systems.
Max says: “Even if we are not sophisticated to be aware of it, there is a pattern, an order, underlying every GO game. Maybe that pattern is like the pattern in the stock market. The Torah. This 216 number.”
Specifically, the number is significant in at least three different ways:

1) The Wall Street agents believe this pattern will unlock the secrets of the stock market.
The agents are working for a predictive strategy firm. They show an interest in Max’s research and convinced him to share his results by providing him with classified computer chip. Max is very evasive but somehow the agents manage to get their hands on one discarded printout that has only part of the number that Euclid spat out. Thinking they have the full pattern, the firm attempts to manipulate the stock market, only to see it crash. Enraged, the agents kidnap Max and demand that he discloses the rest of the code, at which moment he is rescued by Lenny.

2) The Jews believe the number is the key to unlock the true name of God.
Lenny Meyer, whom Max encounters at the café, believes the Torah is just a long string of numbers, a code that was sent to Jews from God. He and his fellow sect members are searching for a pattern in the Torah, which they know is 216-digits long. The leader of the sect explains that according to the Talmud, there was a temple that housed the Ark of the Tabernacle, which contained the 10 Commandments. In this temple, the High Priest would intone one single word: the name of God. The name of God, according to their tradition, was 216 letters long – as many letters as the number computed by Euclid. The Jews believe the 216-digit is the key that unlocks the door to the “Gardens of Eden” and meet God.

3) Sol believes that the number represents the consciousness of the computer.
While Sol was conducting his research on PI he came to the conclusion that certain problems cause computers to occasionally get stuck in a loop, and subsequently crash as a result. A few moments before the meltdown, however, these computers appear to become conscious of their own structure – they become aware that they are made of silicon and other materials.


Now, here’s a crucial point. The number that Euclid displays on the monitor isn’t the 216-digit number everyone is looking for. In fact, the number doesn’t even have 216 digits! It has 218 – go ahead and verify yourself if you like.
I have seen reviews and posts suggesting this might have been a blunder. Honestly, I am very convinced it wasn’t. Here’s why:
1) Aronovsky was careful to describe and display mathematical formulas and ideas very accurately. It’s hard to believe that the production team would have placed so much effort ensuring these mathematical ideas are accurate, but then not have bothered counting the number of digits of a number that is at the epicenter of the story.
2) We never, ever, actually hear Max saying that Euclid’s number is the much sought-after 216-digit number. Viewers are led to believe that it is, but Max never explicitly says it (or anyone for that matter).
3) When Max manages to compute the number a second time (after the trip to Coney Island), he starts writing it down on a sheet of paper. However, after a few digits he comes to a halt as if Euclid’s number has lost its importance. Max realises that the actual 216-digit number is already in his head. Indeed, a few moments later, he is seen attempting to find patterns on a completely different number scribbled on a newspaper page. And guess what, the number on the newspaper is exactly 216 digits! So the number shown on Euclid’s monitor is likely a set of instructions, a kind of recipe, on how to get the actual 216-digit number.
So why the discrepancy? What is the significance of the 218-digit number? What is the relationship to the actual 216-digit number?


Let’s begin with the 218-digit number computed by Euclid. Pay close attention to the digits the camera zooms in shortly before Max passes out (highlighted in red):
94143243431512659321054872390486828512913474876027671959234602385829583047250165232525929692572765536436346272718401201264314754632945012784726484107562234789626728592858295347502772262646456217613984829519475412398501
314 or, if you like, 3.14 – the first 3 digits of \( \pi \). I don’t know if this is a coincidence or not, but the fact that 314 is not the center of the 218-digit number (or even the center of the particular row) makes me wonder why the focus on these particular digits.
It could be that Aronovsky is giving us a subtle clue that suggests this 218-digit number is actually part of \( \pi \).
Remember fact number 5 If \( \pi \) is a normal number, then it’s certain that somewhere within its decimal expansion you will find the 218 sequence shown in the film. Although mathematicians aren’t sure if \( \pi \) is normal, they have a strong suspicion that it is.
At the beginning of the film, Max mentions that Sol stopped caring when he was so close to seeing the true nature of \( \pi \). This suggests that the crux of Sol’s research was writing algorithms that recognise patterns in \( \pi \).
Sol was searching for a pattern within \( \pi \), but a stroke put a definite end to his working days as a mathematician.
\( \pi \) is a transcendental number, it transcends the algebraic tools we have to build numbers (see fact number 3).
As I mentioned above however, maybe there is a pattern underlying this number – a pattern that would finally allow us to understand chaotic structure of \( \pi \).
This is related to the notion that whenever there is a chaotic system, there must be a natural order within its apparent randomness.


In fact, the reason of Sol’s stroke was likely linked to the discovery of the same 218-digit number that Max has found. But why did Max succeeded where Sol failed? One clue is given by the number written at Sol’s apartment after he suffered the fatal stroke. This is the number:
94143243431512659321054872390486828512913474876027671959234603285829583047250165232525929692572765536436346272718401201264314754632945012784726484107562234789626728592858295347502772262646456217613984829519475412398501
At first sight, the number appears to be identical to the one Euclid spat out. However, a closer inspection reveals a difference in two single digits that I highlighted in blue above (compare the two sequences above).
Sol was indeed close, but never really there. Was this a production error? Or did Aronofsky and his team purposely change the two digits in Sol’s note? If the latter, this could mean that attempting to manipulate the wrong 218-digit number could have contributed to Sol’s passing.
Remember fact number 2, all transcendental numbers are irrational, which means that there is no apparent pattern in their never-ending decimal representation.
However, what if encoded in \( \pi \) existed a set of instructions that would allow us to understand all transcendental numbers (those ones that transcend the mathematical tools we have for building numbers)?
This would be big in the mathematical community. The ability to “create” transcendental numbers would likely give us the tools to manipulate nature itself – Max’s ultimate quest.
This is the significance of the 218-digit number. It contains the set of instructions on how to generate the key to deciphering chaotic systems. And everything appears to point that the 216-digit number is the key.
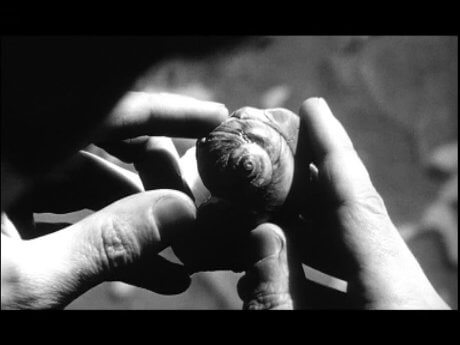

Remember the scene when Max takes a trip to Coney Island, where he notices a few shells with spirals on them on the beach.
This is an epiphany moment for Max. He realises the spirals could represent a way into finding out the secrets of that pattern.
He notices spirals everywhere: in his coffee, in shells, and perhaps more importantly, in the slimy substance that his computer, Euclid, produced before crashing (you can see the spirals when Max looks at the substance via his microscope).


Spirals can be described with the golden ratio, \( \phi \). If you have two lines (one long and one short), and the ratio of the whole line to the longer line is equal to the ratio of the longer line to the shorter line, then the two lines are in the golden ratio (see fact number 4).
\( \pi \) is transcendental and so it transcends the algebraic tools we have to build it. But the golden ratio is not transcendental.
The golden ratio, even though irrational (i.e., has an infinite amount of decimal digits), it is an algebraic number (i.e., a solution to a quadratic equation; see What is algebra?).
Given it’s relationship with \( \pi \), Max could have found a way to unlock the secrets of the number by using the golden ratio as a mediator in the understanding of transcendental numbers such as \( \pi \).
He went back to his research and wrote an algorithm based on the structure of the spiral, which he knows is inscribed everywhere in nature.
When Max has this epiphany, a series of equations are shown, and guess what, the equations contain the number \( \pi \).
Once again, this is related to fact number 4 that \( \pi \) and the golden ratio are related in meaningful ways, and possibly the solution to unravel the mysteries of \( \pi \).
Interestingly, when he runs the algorithm via Euclid, it successfully prints out the 218-digit number it had printed out before.
However, as soon as Max begins to write it down, he halts. Why does he stop? Because he has figured out that the 216-digit number is in his head already – it isn’t the number Euclid is displaying on the screen.
In fact, a few moments later, we see Max trying out different combination of patterns on a completely different number written down on a newspaper page. This number has exactly 216 digits.


In fact, after Max discovers this 216-digit number he has yet another epiphany just as he is about about to kill the ant in his apartment.
He starts reciting some numbers (19 ½, 39 1/8, 6 ¾, 7 & 8, 12 ¼) and says “I know these numbers. They are going down, down, down…”. His mind is getting closer to the truth.
Then he meets with Sol, who immediately realises that Max has figured it out (this is also suggested by Darren Aronofsky himself in the director’s commentary of the film, where he says that in this scene Max “realises he is no longer searching, he has arrived”).
Max found the pattern! That pattern that connects all things in nature. And the pattern is not the actual 216-digit number he had found, but it lies inside his head.
Doesn’t it seem odd to you that nobody has ever come across this number before?
I mean, with the manpower and resources of the Wall Street firm wouldn’t they be able to eventually stumble upon this number? After all, they are the ones providing Max with cutting-edge computer chips.
In fact, Max questions the Jews in this exact same point: surely, they must have written down every combination of digits, translated and intoned them all (well, actually they couldn’t have, see “Would it really be doable to compute every single combination of 216 digits?“).
So, as Max tells the sect leader, perhaps the number is really just a number. What matters is the syntax – the set of rules that lead to that particular arrangement of digits.
The conversation with the Jewish sect is very revealing. Max is convinced that while decoding the pattern he actually saw God.

When he’s trying to figure out the syntax of the 216-digit he’d written on a newspaper page, you can see part of a sentence “(Only God is P…” .
We cannot make out the rest of the sentence, but in the director’s commentary, Aronofsky mentions that it says “Only God is Perfect” and that this newspaper is hidden in other parts of the film.
So it is interesting this connection between the 216-digit number and God.
When he said he might have seen God, he could be referring to the moment when he realised the actual 216-digit long number is already in his head. Remember when he started writing down the number Euclid computed, but then stopped after jotting down a few digits?


Shortly after realising the number was in is head, he has a terrible headache and the white void appears. This white void is also present just before the drill scene, where Max is standing in a completely white room in apparent tranquility, reciting seemingly random numbers.
Aronofsky mentioned in the director’s commentary that Sean (the actor portraying Max) should have done this scene completely naked. They decided against it, however, because Aronofsky thought it might be too distracting.
Still, the fact that Max should have appeared naked in this scene (perhaps as a parallel to how God created an also naked Adam) could represent Max’s purity of mind.
Could the white void represent the transition to enlightenment? The purity of mind he so long aimed to find?
If it does, it is obvious that Max now understands that this quest is ultimately destroying him.
He gets rid of the evidence by destroying his research tools and burning Sol’s research notes, and engages in trepanation to remove what he believes to be the source of his knowledge and pain – the vein above his right ear.
It is natural that humans attempt to understand the world around them: generations of thinkers and scientists have done so. Max, however, takes this quest to the limit, as he believes that there is an implicit pattern in everything in nature. Everything is therefore connected via this pattern: an organism of sorts, represented by a 216-digit number.
As Max gets closer to this fundamental Truth, his mental health deteriorates to the point that he begins to conflate reality with fantasy.
The film leaves us with the ambiguity of whether Max did in fact decode the pattern. Because the main character, Max Cohen, appears to suffer from Psychosis, it is unclear what/who is real and what/who is simply a figment of his imagination.
Perhaps he did, but feels that he cannot bear such responsibility and knowledge. Perhaps he did not, and the drilling was the act of a desperate man that recognised the limitations of the human mind. I guess we will never know.
Max’s final drastic behaviour is perhaps a reflection of the sobering reality that the human mind is simply not equipped to deal with this kind of knowledge. Perhaps it is better to be incognizant of the true meaning of life, and simply take joy in watching the leaves of a tree being blown by the wind.
Mathematicians have proven that transcendental numbers (to which \( \pi \) belongs) are more numerous than numbers we are familiar with (see fact number 7). In a way then, \( \pi \) isn’t particularly special or unique. Claiming that \( \pi \) contains within it the pattern that explains every natural phenomenon, would be like saying that the genome of a cat contains everything necessary to understand all living organisms.
Perhaps this is true to a certain extent. Genetic differences between the cat and human species naturally vary, but you would be surprised to know that we share about 90% of the genes with the domestic cat.
So, perhaps the focus on \( \pi \) is meant to represent that crucial anchor to which all numbers are linked to. Maybe there exists a certain interconnection between all transcendental numbers that mathematicians have yet to discover. Think of how the 100 billion neurons are interconnected to support most of the operations of the brain, or how dark matter connect the two trillion galaxies across the entire universe in a gargantuan galactic dance.
I’m digressing, I know, but it is surely fun to speculate! 😉
See you in the next article!
Leave a comment
Add Your Recommendations
Popular Tags