This post is part of a larger deep dive
Curious about the role of the infinite universe in Another Earth? Check out Another Earth Explained!
Or read the full Another Earth article!
This post is part of a larger deep dive
Curious about the role of the infinite universe in Another Earth? Check out Another Earth Explained!
Or read the full Another Earth article!

Ahhh, the universe, my favourite topic!
One question that has always bothered me though has been: what lies beyond the universe? Have you ever thought about it?
If not, here’s another question for you: imagine you were immortal and had a space rocket with a perpetual source of fuel. What if you set out your one-way ticket journey from Earth into unknown space? Would you ever hit a “wall”? If so, what would there be behind that wall? More space? What if you climbed the wall and continued your journey, would there eventually be a wall you could not cross? But if there is a wall you cannot cross, what is there behind that wall?
As a teenager, it was these sort of questions that filled many of my afternoons (I was a weird kid!).
Some astronomers are fervent believers that space extends infinitely. That is, if you fired your rocket you would never hit a wall, you would just go on forever and ever.
As we will see shortly, if you believe the theory of an infinite universe, there is nothing in the laws of physics that prevent multiple yous living on a planet they call Earth, reading this very same sentence you’re reading. In fact, in an infinite universe there would be an infinite amount of yous. Some would have lives identical to yours, some would be leading very different lives.
But in order to understand why, you should first be familiar with at least two concepts in astronomy: the expansion of the universe and the Big Bang.

When astronomers look into the sky with their telescopes, they are looking at the past.
That is because light has a finite speed (300,000 km per second), and therefore it takes some time for light emanated from astronomical objects to reach our eyes.
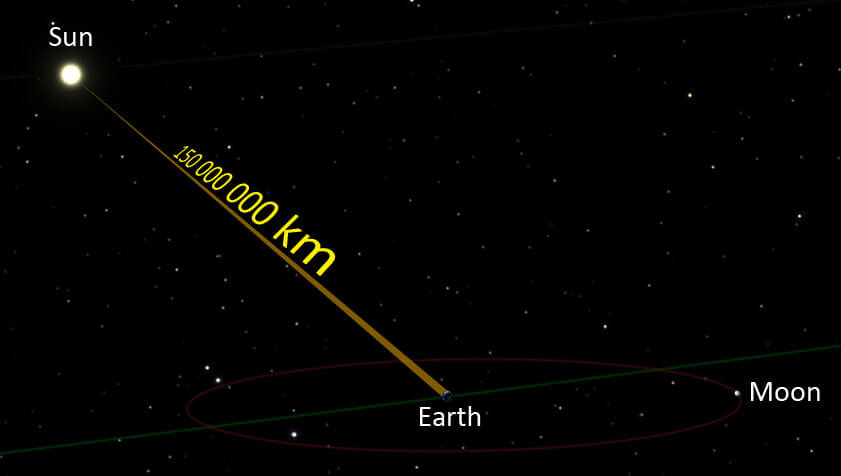
For example, the sun is at a distance of 150 million km from Earth. So, the light the sun emits at this moment (which is traveling at 300,000 km/sec) will need about 8 minutes to reach our eyes.
So when you look up at the sun, you are seeing the sun when it looked like 8 minutes ago.
The general formula for calculating how much time something takes given a certain distance and velocity (assuming constant velocity) is:
\( time = \dfrac{distance}{velocity} \)The distance between the sun and the Earth is 150 million km, so \( distance = 150,000,000\: km \). The speed of light is \( 300,000\: \text{km/s)} \)
\( time = \dfrac{150,000,000\: km}{300,000\: km/s} \)\( time = 500\: seconds \) (or 8,3 minutes)
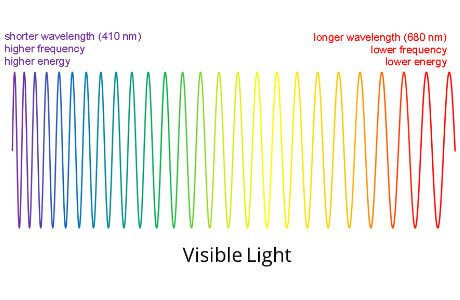
Light travels through space in the form of a wave. If light waves are long (or stretched out), light will appear reddish. In contrast, if light waves are short (or squashed), light will appear blueish.
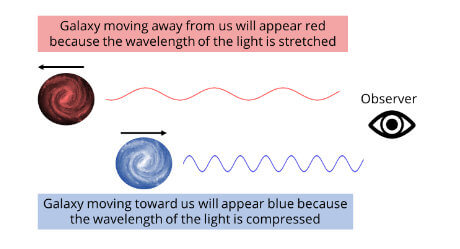

When astronomers look really, really far away in the sky, at the edge of what the most powerful telescopes can detect, what they see is that every galaxy is glowing red. What could this mean?
The light waves emitted from a galaxy or a star don’t have to stay the same length; they can be squashed (they will have a shorter wavelength and move towards the blue end of the spectrum) or stretched (they will have a larger wavelength and towards the red end of the spectrum).
So, scientists concluded that the reason the galaxies at the edge of the observable universe appear red to us is because space between us and these distant galaxies got stretched. Because space got stretched, the light that was given off by these galaxies got stretched as well on its way to us.
The logical conclusion from all this was that our entire universe is expanding.
To visualise what stretching of space means, think of the universe as the surface of a balloon with dots drawn on its surface representing the galaxies.
If you blow air into the balloon, it will expand, and the dots (the galaxies) will move away from each other.
So, when you blow air into the balloon, you are not adding new rubber to the balloon. Similarly, when space is stretched it doesn’t mean you are injecting new matter into the universe. Rather, it’s the fabric of space itself that is stretching (just like the surface of the balloon).
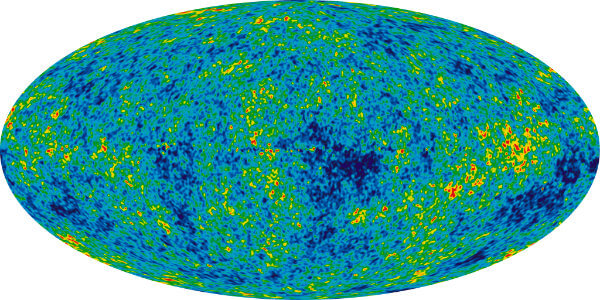
Now, as space continued to stretch, the wavelengths of light emitted from the very first galaxies got stretched so much that they went out of the light spectrum the human eye is able to detect. This light has been transformed into radio waves and microwaves. Scientists have been catching residues of this microwave light, which is known as Cosmic Microwave Background (CMB).
Cosmologists then posed an interesting question: if the universe is expanding, does that mean that if we could rewind the evolution of the universe, all matter in the universe would be closer together in the past? What if we continued to rewind? Will all matter be confined to a single point?
Two words: Big Bang!
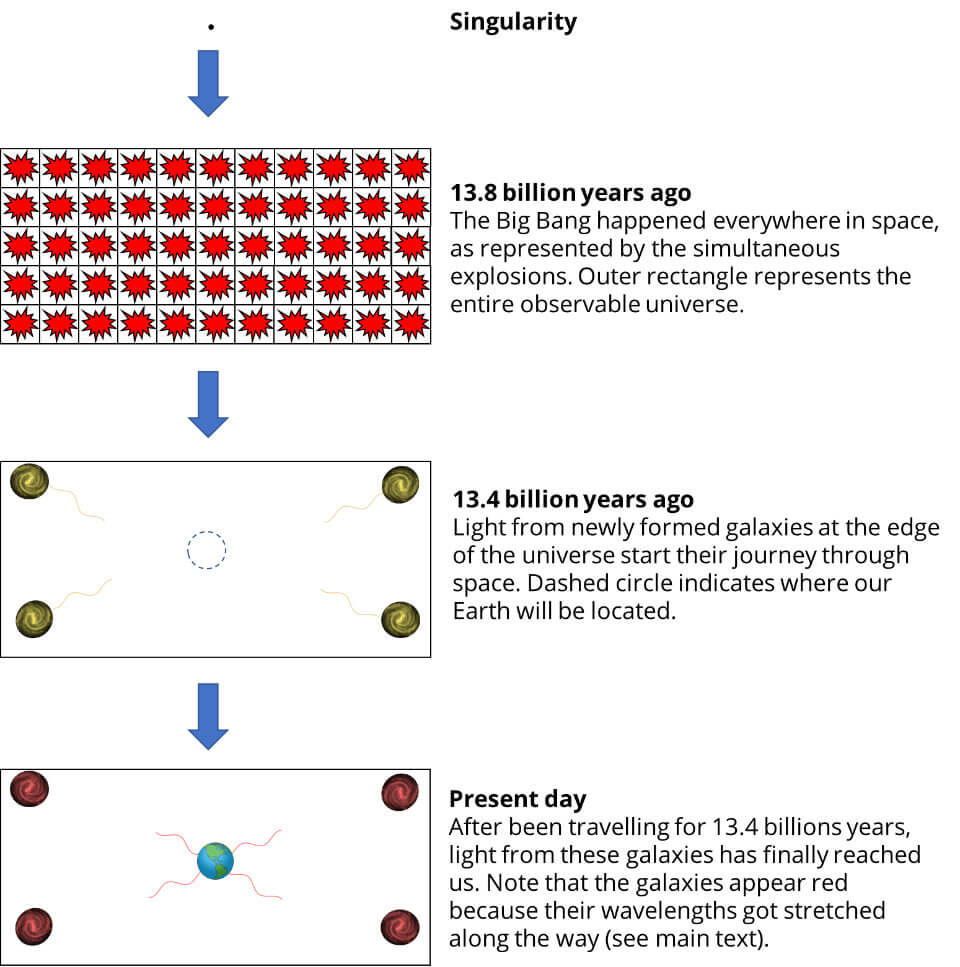
The image of the Big Bang that has been overly popularised is that of a single point that explodes and shoots off matter everywhere in all directions. For years, this was the image I had about the Big Bang, but it couldn’t be more wrong.
The problem is that this idea falsely suggests that there was a specific place where the explosion occurred and that matter simply flung out from this focal point. This is wrong! The Big Bang, as scientists understand it, did stem from a tiny point of unbelievable density (a singularity) that expanded very rapidly. But it happened everywhere, and at the same time.
For me, it helps thinking of the big bang, not as a single explosion from a single point, but that of many, many little points exploding simultaneously, as the figure above illustrates.
So, galaxies are flying away from us not because the big bang hurled them into the void of the cosmos, but because space itself is stretching.

You may wonder that if the Big Bang created the entire universe, how much of it did it create?
One point I want to get out of the way from the get-go is that an infinite universe doesn’t imply infinite types of particles.
Imagine an infinite deck of playing cards. Even though you have an infinite amount of physical cards, the types of card are not infinite. In a standard 52-card deck there is an ace, numerical cards 2-10, a jack, a queen and a king in four different suits (clubs, hearts, spades and diamonds). So, if you kept drawing a card from your infinite deck of playing cards, the type of card would be bound to repeat.
The reason scientists believe that there are a finite amount of particle types in the universe has to do with the notion of the cosmological principle.
The cosmological principle states that the universe will appear uniform when viewed on the largest of scales. That is, no region in the cosmos is more special than the other.
You might argue “but what about our solar system, we’ve got Earth, the Sun, the other planets, surely that is special”. However, according to Albert Einstein, these are simply irregularities that can be largely ignored.

Let’s say you took a jar containing 100 million light-years of space stuff. Let’s call it Jar A. Now go to another corner of the universe and place 100 million light-years of space stuff into Jar B.
If you averaged the amount of galaxies, amount of matter, temperature, an so on in each jar there would be hardly any difference between the jars.
In fact, if you took 1 million jars they would all look identical. So the most obvious conclusion from this is that on a very large scale (100 million light-years across) space is pretty much uniform (i.e., it has the same kind of “stuff” everywhere).
Astrophysicists are happy to accept the cosmological principle as true (even though there are also reasons to believe it isn’t) because it makes Einstein’s equations of General Relativity far easier to solve – if the equations are applied to a uniform universe, they are essentially reduced to only one!
The implication of this is that no matter where you look within the observable universe (which has a radius of about 46 billion light years) we see that it contains pretty much the same types of matter. Look to the left and you’ll see types X, Y and Z. Look to the right, and you will still see X, Y and Z.
So it’s not a stretch to think that if the universe is indeed infinite, the same types of matter may exist everywhere in the entire universe (observable and unobservable).
The point I’m trying to make is that we can have a universe that extends infinitely with types of matter that are finite. And if types of matter are finite, the possible arrangements of those types of matter are also finite.
To make this a little bit more tangible, let’s say you are interested in finding all possible triplets consisting of letters X, Y and Z. So the arrangement XXX is one possible triplet, XYZ another triplet, YZZ another triplet and so on.
In this case, there would be 27 possible unique triplets; 27 ways letters X, Y and Z could be arranged in threes:
XXX, XXY, XXZ, XYY, XZZ, XYX, XZX, XYZ, XZY
YYY, YYX, YYZ, YXX, YZZ, YXY, YZY, YXZ, YZX
ZZZ, ZZX, ZZY, ZXX, ZYY, ZXZ, ZYZ, ZXY, ZYX
You can extend this reasoning by replacing letters with particles and triplets with universes. Of course, there are many many particles in the universe, so the number of possible configurations for all of those particles is enormous.
Impressively, scientists have actually calculated the possible number of distinct configurations of particles in our universe. As it turns out that number is about \( 10^{10122} \). This a mind-boggling number that is beyond human comprehension; just for reference, the number of atoms in the observable universe are a measly \( 10^{82} \) (or 10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000).
Still, however huge \( 10^{10122} \) may be, it is still a finite number.

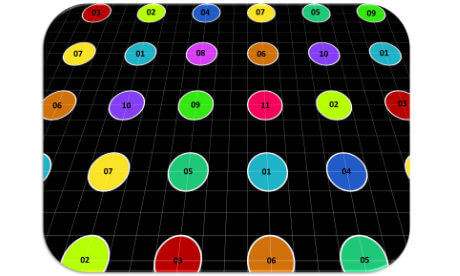
Imagine there exists an omnipotent being (let’s call her Dottie) with a bag of \( 10^{10122} \) universes in the shape of lotto balls. Dottie’s only job is to pick up a lotto universe and place it here and there in the infinite expanse of space.
Let’s also imagine that out of those \( 10^{10122} \) possible universe arrangements, our particular “lotto universe” is number 5.
Dottie draws the first lotto universe and it’s number 1021002. Second lotto universe and it’s 9993999892839. Third one is \( 10^{13} \), and so on and so forth. Our lotto universe (5) will eventually be picked, and there will be a point that no lotto universe is left in the bag.
Now, Dottie cannot be out of a job (there’s still plenty of space to cover – after all, it is infinite), so she grabs a new set of balls, puts them in the the bag and starts all over again. In fact, since the space with which she is working is infinite, she needs to keep drawing lotto universes an infinite amount of times, meaning that our universe (number 5) will also be picked an infinite number of times.
To state the obvious, in a universe that expands infinitely, but with a finite number of particle arrangements, there will be an infinite number of universes with worlds that look exactly like our Earth, with people that look exactly like us, and are doing the exact same things we are doing!
BOOM!!!!
It’s true that the greater amount of particles you have, the greater the number of possible configurations.
So, you could argue that perhaps universe 102 will have twice the number of particles than our own, universe 14 will have three times the particles of our own, and so on.
If this were the case, the universes might never repeat, because each could contain a different amount of particles, and hence either more or less possible arrangements of matter.
But here is the key: particles carry energy, so that means the more particles you place in a universe, the more energetic it becomes. And if a region of space has too much energy it will eventually collapse on itself and form a black hole.
The way I think about this is to imagine a paper bag that can hold a maximum weight of 4 kg. Place one milligram more and the paper bag tears.
Now, let’s assume an infinite source of potatoes, carrots and blueberries. If you put too many potatoes in the bag, say 21, the bag will tear. So there is a limit to how many potatoes you can place in the bag (up to 20 potatoes).
Let’s do the same with the carrots and blueberries and assume that the paper bag can hold up to 50 carrots or up to a 1000 of blueberries without tearing.
Great! We have established that 4 kg is equivalent to 20 potatoes or 50 carrots or 1000 blueberries.
Now, you cannot add 20 potatoes and 1 blueberry, because that extra blueberry will exceed the 4 kg max the paper bag can hold. So you can add 19 potatoes and 1 blueberry, that’s allowed, because it will be below 4 kg.
This means you are free to recombine potatoes, carrots and blueberries at your leisure, so long as their combined weight does not exceed 4 kg.
This constraint is what makes the possible arrangements of food stuff finite, even though there is an infinite amount of it.
You can think of the universe as a paper bag and the particles contained in the universe as the foodstuff. Even if there are an infinite amount of particles, within any given stretch of space (say the size of the observable universe, or about 93 billion light years across), there must be a finite amount of energy (similar to the 4 kg max of the paper bag). The particles within this space are free to recombine so long as they don’t go over this energetic upper limit.
The point to take home is that there is a limit to how much energy the universe can contain. Finite energy necessarily entails a finite number of particles, and a finite number of particles necessarily entails a finite number of configurations of those particles.
The maximum amount of configurations for the observable universe appears to be \( 10^{10122} \).

Before you decide to point your telescopes up in the sky, hoping to see another version of yourself, let me be the killjoy of the party to inform you that it will be a fool’s errand.
For fun, let’s see if we can grasp just how long it would take to create a universe that would look just as ours using our notion of time.
To warm you up for this task, think about a deck of 52 cards first. The 52 cards can be arranged in 80,658,175,170,943,878,571,660,636,856,403,766,975,289,505,440,883,277,824,000,000,000,000 ways. Let’s say we are only interested in one configuration: the original configuration that comes in the box (Ace, 2-10, Jack, Queen, King, first in clubs, then hearts, then spades and finally diamonds).
Assuming that all deck configurations are equally likely after each shuffle, if you picked a configuration every second, it would take about \( 8 \times 10^{67} \) seconds to get the one you wanted just by chance.
Well, the age of our universe is \( 5 \times 10^{17} \) seconds. And \( 5 \times 10^{17} \) seconds is way shorter than \( 8 \times 10^{67} \).
So it would take billions and billions and billions of “universe ages” just to draw the one configuration we wanted! And we are only working with a mere 52 cards.
The universe, however, has many more particles than 52. In fact, as I mentioned above, the amount of configurations for the particles in the observable universe is about \( 10^{10122} \), which is way, way, way more than the amount of possible configurations in the 52 cards.
So, the time you would have to wait to see another universe that looked exactly like ours is simply unimaginable, and the probability that it would be created in the vicinity to ours is practically 0.


If your head hurts from all this, don’t panic. The key point is that with an infinite universe, you are guaranteed to have infinite repetitions of our observable universe. However, these realms are so, so, so, so, so, so, so, so distant from us that the expansion of the universe far outpaces the time light from these worlds will have time to reach us.
And if light isn’t able to reach us, no information at all can be exchanged between realms. Each realm is confined to its own cosmic horizon – the extent of space where interactions within the patch are possible (see figure above).
Famous astrophysicist Dr. Brian Greene suggested that our universe could be a bit like a patchwork quilt. Space would be filled with a multitude of universes (the patches) with their own independent cosmic horizon.
Even though our patch and other parallel patches inhabit the same physical universe, they are, for all intents and purposes, completely independent realms that will never ever have a chance to meet.
Boohoo…
Great article! A question is the rotation of Earth 1 and Earth 2, and what they see of each other because of their different positions in relation to the Sun. I guess Rhoda 2 could not see Earth 1 (lit by the sun) through her car window and therefore did not cause the accident.
Hi Andreas,
Yes, that’s a very good observation!
Indeed, I agree that Rhoda 2 couldn’t possibly have been looking at Earth One at the time of the accident. For that to happen, the American continent of each Earth would have to be facing each other, and that would imply that the American continent of Earth Two had to be facing the sun, in which case Earth One wouldn’t be visible at all.
I mentioned somewhere in the article that synchronicity probably broke as soon as Earth One inhabitants caught sight of Earth Two, and that must have happened way before the accident.