Quantum mechanics
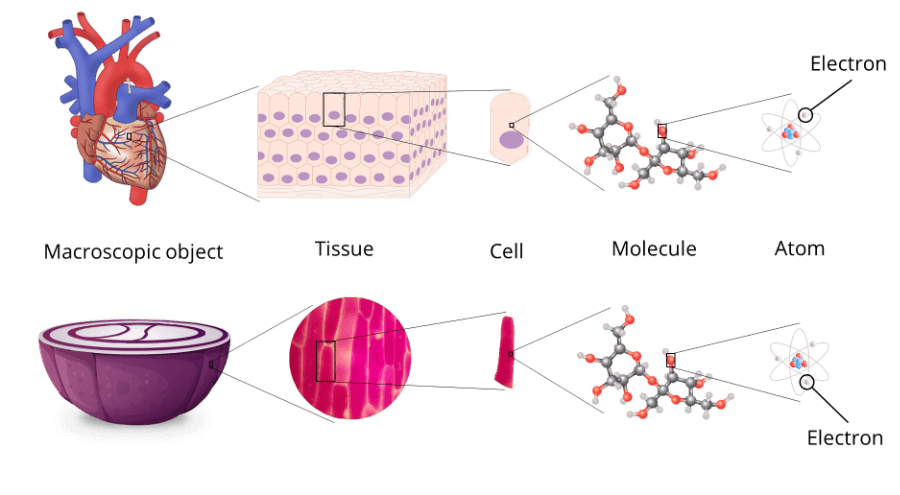
When you think of physics, your might immediately visualise things like the motion of planets, balls rolling down slopes, levers and so on.
In fact, most of the physics of everyday objects can be accurately described by classical laws of physics, such has those put forth by fellows like Isaac Newton and Albert Einstein.
But dive into the realm of atoms and subatomic particles (i.e., the tiny stuff that make up all matter such as protons, neutrons and electrons), and the classical laws are pretty much useless.
You see, if you run an experiment twice without changing any aspect of the experiment whatsoever, you expect to get identical results according to the laws of classical physics.
With macroscopic objects that is true.
With the micro-world classical physics fails miserably.
Predicting the location of quantum particles
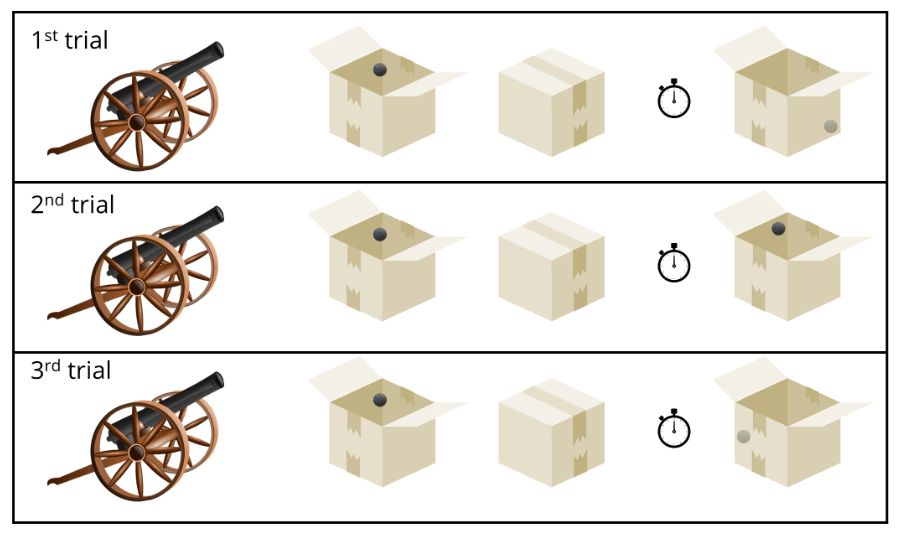
Imagine we decide to run an experiment in which we shoot electrons into a box, and after exactly 5 minutes we measure its location (see figure above). Let’s say we detect it at the lower right corner of the box.
Good! Now, repeat the same experiment in the exact same way.
Logic tells you that you should detect the electron in the lower right corner, right? However, this time it might be detected at the top left of the box. Repeat the experiment, and the third time it might be detected in the middle left corner.
In fact, you will never be able to predict where the electron is located. Never!
Now you might argue: “Wait, wait, wait, wait. I know Google is working on a quantum computer, and that deals with those electron thingies and whatnot. So how can they create complex stuff like computers from something so unpredictable like electrons?”.
I said you cannot predict the location of electrons based on a single measurement. There is, indeed, a way to check for regularity, and that comes in the form of probability.
(As an undergraduate student, statistics was one of my favourite topics at university. My colleagues found me weird, and the feeling was reciprocal. Why wouldn’t anyone find statistics interesting?)
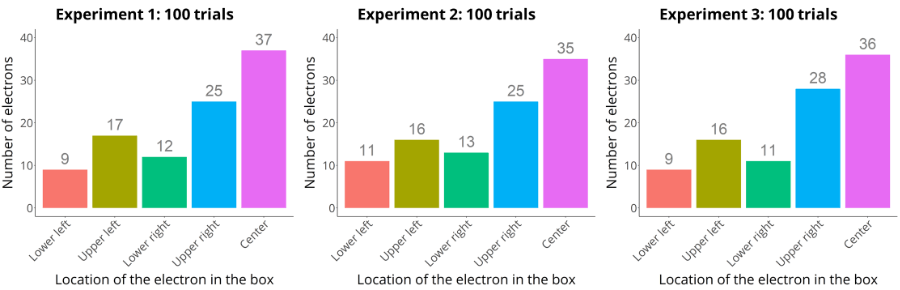
Back to the electron.
If you take 100 measurements of the location of the electron in the box, you can compute something called a distribution. In the case of the electron experiment, it really just means counting the amount of times the electron appears at several places in the box and plot the values (see figure above).
That distribution might tell you, for example, that 9% of the electrons (9 electrons) are in the left lower corner, 17% (17 electrons) in the right lower corner, 12% (12 electrons) in the left upper corner, 25% (25 electrons) in the right upper corner and 37% (37 electrons) in the center.
Now take once again 100 measurements of the location of the electron using the exact same set-up.
If you plotted the distribution of those newly 100 measurements, you would likely see a similar distribution as the first sample.
Thus, we cannot predict the exact location of the electron in any single measurement, but we can determine the likelihood of finding the electron at any specified location.
For example, I can now say something like:
“I can’t predict the exact location where the electron is located, but I can say that there is a 37% chance that it will be located at the center”.
The double-slit experiment
OK, so we have established that you cannot predict the location (or any other property really) of quantum particles, such as an electron, using single measurements, but you can get an estimate using probabilities.
The world of physics is filled with cool and groundbreaking experiments, but, to me, the double-slit experiment ranks among one of the most phenomenal experiments that led to the most outright bizarre results I have ever seen.
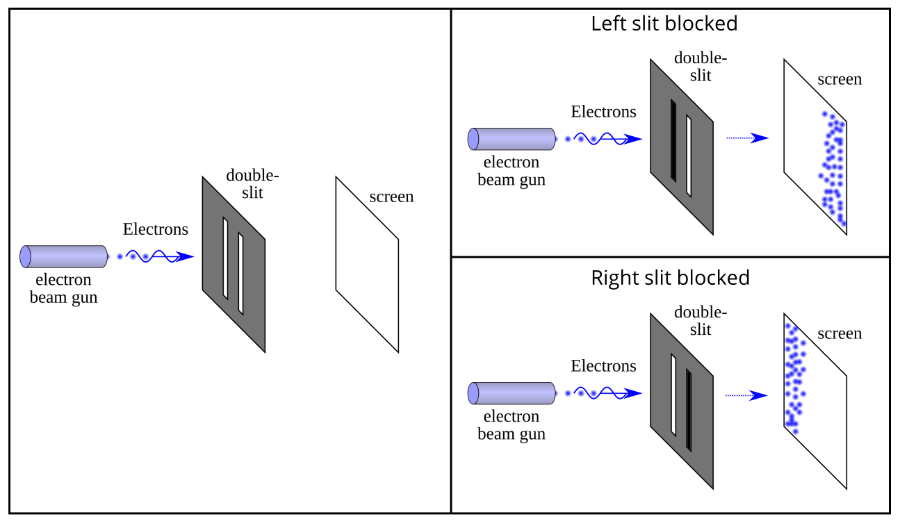
The set-up works more or less like this: Imagine you have a barrier with two slits which are separated by less than one millimeter (see left figure above).
Next, you shoot electrons from an electron gun and measure where they hit on a detector screen placed behind the barrier with the slits.
First, let’s close the left slit and shoot one electron at the time. The top right figure above shows what happens.
As you would expect, they accumulate on the left side of the detector screen – there is a bit of spread because some electrons pass right in the middle of the slit, some bump on the slit and change course, etc.
Now, close the right slit now and shoot electrons through the right slit. What happens? That’s right, you see their trace on the right side of the screen (see bottom right figure above).
OK, nothing terribly exciting about this. But what happens if we open both slits?
If your answer was: “well, obviously the result should be a combination of the two”, oh boy, are you in for a surprise!
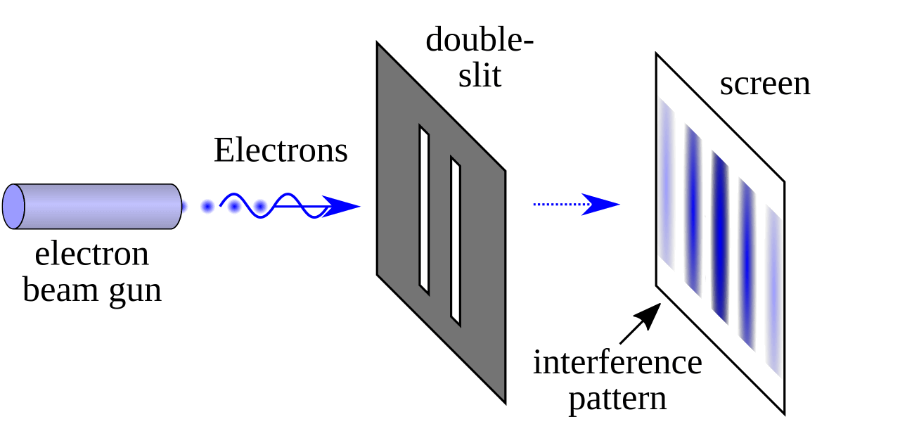
The result scientists actually find is shown in the figure above.
When they shot electrons one-by-one when both slits were opened, they observed a series of light and dark bands which corresponded to the places where electrons either hit the detector screen (light band; in the figure above that corresponds to the blue bands) or did not hit the detector screen (dark band; in the figure above that corresponds to the white bands).
Huh?!?, weird…
Why the heck aren’t we seeing a combination of patterns when either slit is opened? How did these dark and light stripes came to be?
As it turns out, the black and white stripe pattern is called an interference pattern, and to physicists it can only mean one thing: waves.
Surfing on the wave function
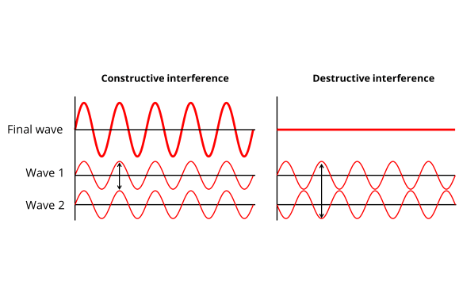
Think of the wavy pattern that you get when you throw two rocks side-by-side on a pond.
If the peaks of the waves overlap they will form larger waves.
If the troughs (or valleys) of the waves overlap they will form larger depressions.
If a peak of a wave overlaps with the trough of another wave, they will cancel each other out. This is exemplified in the right figure above.
Now, imagine you’d placed a detector screen at some distance from the origin point of the waves (see left figure above). Once the waves interacted and hit the detector screen, it would show a bright spot whenever a wave was high, or a dark spot if there was no wave.
Do you notice the similarity with the pattern we get for the electron when both slits are opened? There is no denying.
This can only mean that the electrons in the double-slit experiment are behaving like a wave.
If the peaks of the waves of the electron overlap, you will get a bright band on the detector screen.
If the peak and a trough meet, the two will cancel each other out, and you will get a dark band on the detector screen.
But what exactly is this wave? What is it made of?
Even though I encourage you to visualise the electron wave as an actual wave, it is actually not a physical wave. It’s purely mathematical, and it’s called a wave function (or probability wave).
The wave function of the electron defines the likelihood of the electron being at a particular location.
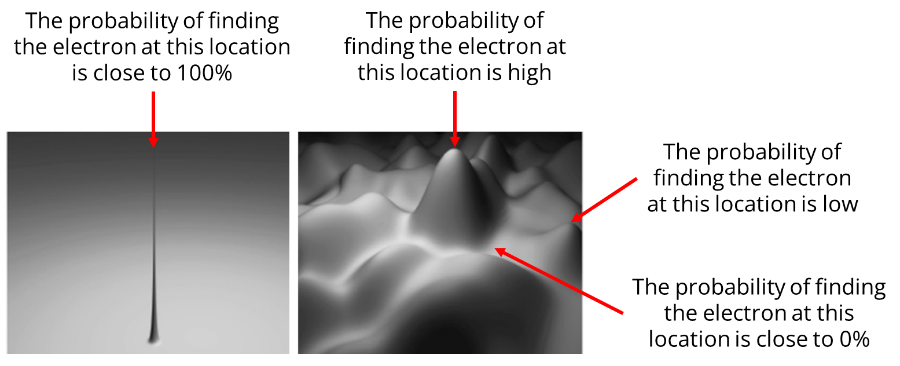
If the value of the wave function is high (near its peaks) at a certain point, the more likely it is that the electron will be found there. As the wave moves across time, the values of the wave change, going up at some locations and then down at others.
If there were only one peak in the wave function like in the left figure above, we would know with almost 100% certainty where the electron would be located.
However, for quantum particles, the wave function is way fuzzier and spread out like in the right figure above.
A big old question is what happens to the wave function when it reaches the detector screen?
The wave function arises when a quantum particle is moving – think of a wave moving through the slits as in the video above.
Part of wave goes through the left slit, part of the wave hits the middle of the barrier, and part of the wave passes through the right slit.
And remember, the electron gun is firing one electron at a time, so each electron must be transformed into this wave function that doesn’t exist in physical space (it’s only mathematical).
Now, because the wave passes through both slits, they will form one wave in the left and one wave in the right slit, so they will interact with each other.
This means that the wave of the electron is interacting with itself (this is the reason why people sometimes colloquially say that the electron is passing through both slits at the same time – actually it’s its wave function).
When the wave function is about to hit the screen, the landing position of the electron is determined by its value in the wave function: if the value is high, it’s likely to be a landing place, if the probability is low, there will be a very low chance we will find the electron there.
So, in some way, the wave function is the electron itself, and where there is non-zero probability, it is a possible location for the electron to be at.
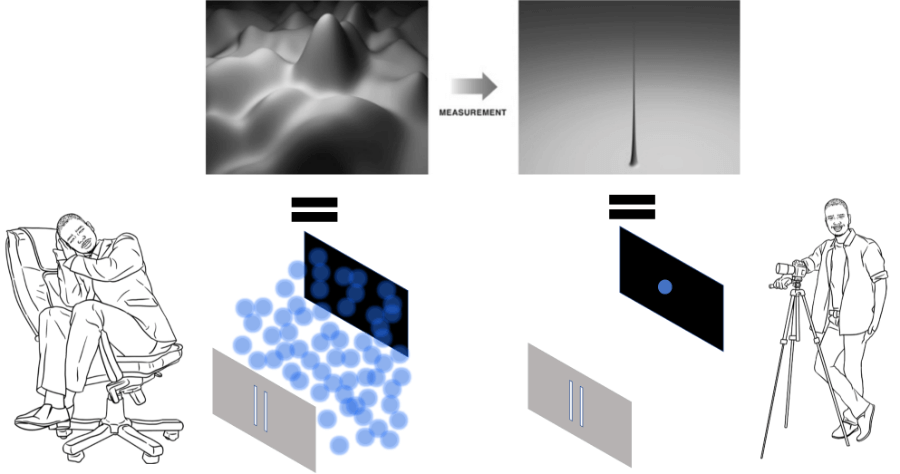
According to a popular hypothesis, whenever we are not observing or measuring the location of the electron, the electron can be described by its wave function (it is everywhere where the wave function is non-zero).
However, as soon as the wave function touches the detector (or someone makes a measurement), it collapses into a single spike – the electron itself, which is shown as a dot on the screen.
This is exemplified in the figure above. Note how the wave function is reduced to a single spike when it meets the detector.
This interpretation has come to be known as the Copenhagen interpretation, first proposed by Niels Bohr and Werner Heisenberg.
However, the Copenhagen interpretation is at odds with very solid quantum mechanics mathematics.
Specifically, the Schrödinger’s equation – which forms the mathematical basis of quantum mechanics – does not allow waves to collapse. Schrödinger’s math is able to explain many phenomena with incredible accuracy, so there is no reason to believe it is inadequate to explain the change from the wave function to an actual measurement.
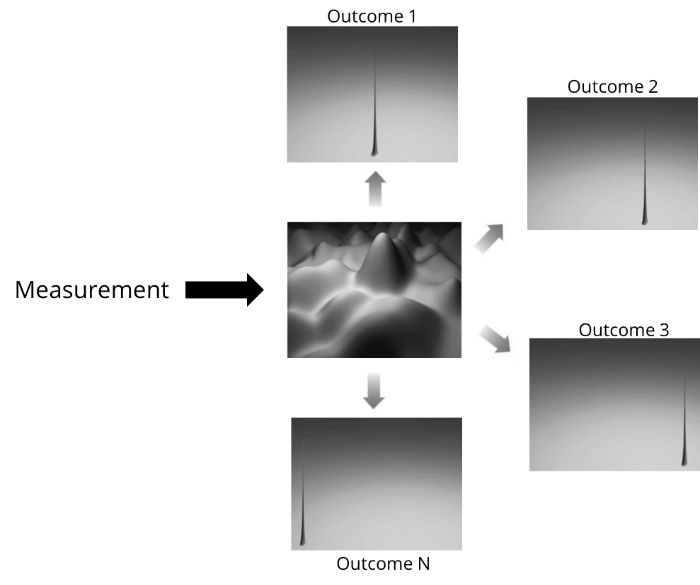
But, then, if the wave function does not collapse, why do we only see one dot and not a multitude of dots where the wave function has a non-zero probability?
Many-worlds interpretation
When faced with a wave function with spikes of different heights, Schrödinger’s math tells us to combine the results.
This is akin to having an equation such as \( x^2 + 5x + 6 = 0 \) which can have two solutions: -2 and -3.
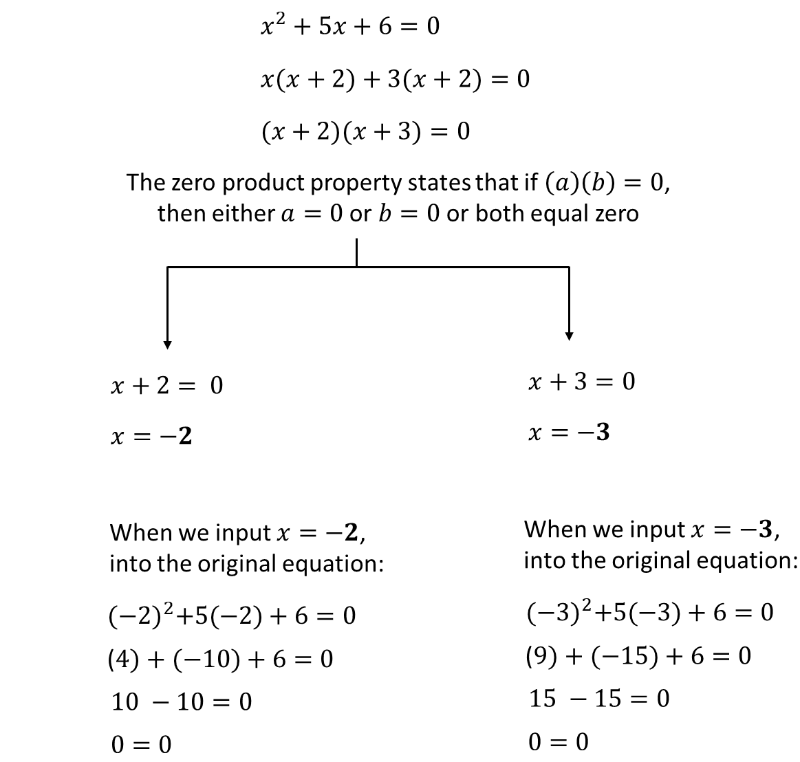So, there are two solutions (or roots) to the quadratic equation \( x^2 + 5x + 6 = 0 \): -2 and -3.
Schrödinger’s equations are similar in this respect, in that it gives us multiple solutions when we input the wave function of a quantum particle.
Now, the implication of this is that if we make a measurement, and if the wave doesn’t collapse, then the measuring device (and, by extension, our brains) should register multiple locations at once.
But, surely, that’s silly, and not what we experience in reality. If you fire only one electron towards the screen, the detector (and your brain) only registers one dot on the screen, not many dots simultaneously.
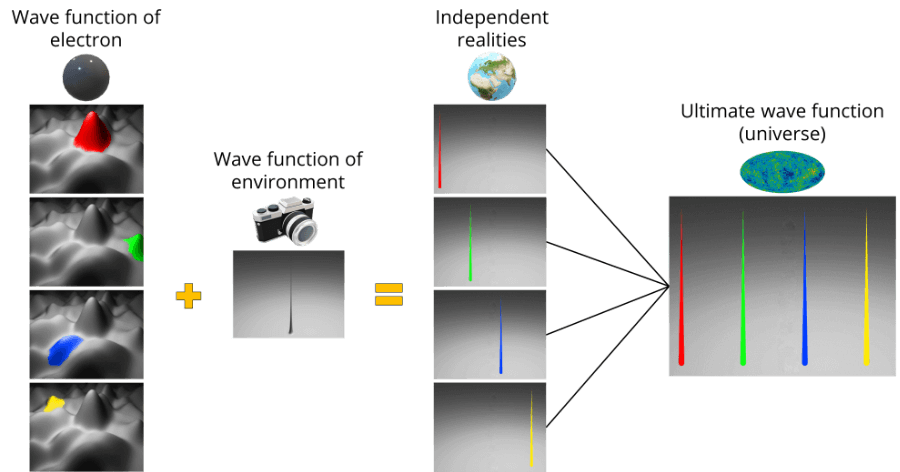
While writing his doctoral thesis in 1957, Hugh Everett had a phenomenal insight.
He speculated that the reason we are not experiencing all outcomes at once is because every time you make a measurement the device “splits” into different timelines, each with a different outcome.
So, if the wave function of the electron has 100 peaks with non-zero probability, then, upon measurement, there will be 100 devices, each showing one of the 100 possible locations of the electron.
But remember that we are also made of particles, the lab where we do the experiment is made up of particles, the entire universe is made up of particles.
What happens then is that the wave function of the electron gets mixed up with the wave function of everything else in the universe, giving rise to another wave function: the ultimate wave function.
Using slightly more technical wording, the electron and the environment (which we are part of) have become entangled. The result is distinct, isolated states, which form independent realities. This is called decoherence.
Many explanations of the Many-worlds interpretation make use of phrases such as “the universe splits”.
We should refrain from such phrasing because it gives the (wrong) idea that there are actually universes being created out of thin air, which is completely counter to what the Many-worlds interpretation is proposing.
No, the universe doesn’t split.
Rather, there is only one universe which is defined by the commingling of the particle’s wave function with the wave function of the environment (the ultimate wave function).
The ultimate wave function can be decomposed into separate independent “branches” that originated from the decoherence process (i.e., when a measurement was made, all outcomes given by the wave function were realised in different timelines).
So, there is only one ultimate wave function (i.e. one universe) with different spikes representing independent timelines.
In other words, rather than having parallel universes, each with its own matter, we have one universe within which different timelines are evolving completely independently.
Everett also pointed out that his proposal can be generalised to any measurement. If a split occurs and one of these yous does another similar experiment, that world would split again into many other worlds, and so on…
I hope you see where I’m going with this.
If upon measurement of a quantum phenomenon our timeline splits, then that means that there are a really huge number of worlds “emerging” every second.
You might think that splitting will be rare since only physicists do double-slit experiments.
However, Everett’s proposal is general, and applies to every quantum particle that is confronted with a choice – particles in your own body can cause a split, particles in the north pole can cause a split, particles in the Sun can cause a split, particles in another galaxy can cause a split, and so on and so forth.
This means that there are (perhaps) an infinite number of timelines.
And let’s be completely clear. None of these universes is any more real than the other. As soon as a quantum measurement is made becomes entangled with the wave function of the quantum particle, resulting in a multitude of independent realities.
Problems with the Many-worlds interpretation
You may have noticed that in the Many-worlds interpretation of quantum mechanics, everything that is possible to happen will be developed into its own world. By “everything”, I mean outcomes with a non-zero probability.
But here is the catch: if every single outcome occurs, even those with little probability of occurring, then what do the probabilities of the wave function actually mean?
If the wave function tells us that the electron is 50% more likely to be found at the top right, 45% on the top left, 4.9999999999% at the bottom right, and 0.00000000001% at the bottom left, then we can assume that it’s really, really, really unlikely that the electron will be seen at the bottom left.
However, according to the many-worlds approach, 0.00000000001% is still a non-zero probability, so the electron will definitely show up at the bottom left in some world.
Everett responded to this criticism by claiming that probabilities enter the Many-worlds but in a very subtle way.
To understand his reasoning, consider this thought-experiment that I read in the book “Hidden reality” by Brian Greene.
Imagine that a race of aliens come to Earth and tell you that they will create a copy of yourself while you sleep tonight. This copy will be exactly like you in every single respect but will live in a parallel timeline so the two of you won’t interact. In fact, both of you would think they spoke with the aliens, and both would be right.
The aliens also say that on the next day, they will grant one of you a wish of your choosing, whereas the other will be taken to the aliens’ world and become their slave.
A 50% chance that you will become slave is too much of a risk for any sane person, so you would probably reject the offer.
OK, let’s say now that the aliens make another offer. They will create one million copies of you and will grant a wish to 999999 of yous, but one of you will still become a slave.
Now, what do you do? The likelihood that you will be picked is very very very tiny – almost zero. So you might think, why not.
Hah! But therein lies the problem.
It will be absolutely certain – 100%! – that you will end up being a slave, because the unlucky you will also be you!
So, before the cloning actually takes place, it makes no sense to speak of probabilities, since it is a given that one of you (and, so, you) will become a slave.
Contrast this when morning arrives. As you open your eyes, you start pondering what are the odds that you will be flying away as the aliens’ slave.
Because now you are a separate being, distinct from the other yous that inhabit the other timelines, it makes sense to talk of probability. You can now say that the chances of this particular you ending up a slave are 1/1000000, and realise that this is indeed a very small chance.
Applying this to the the double-slit experiment, when you are not observing the electron, you know it exists at every location. You also know that when you make a measurement, every outcome will be realised in different timelines, so one of you is guaranteed to see the electron in a particular location. In this case, it doesn’t make sense to talk of probabilities, because there is 100% certainty that the electron will be in every location in at least one of the timelines.
When you make the measurement though, you can ask yourself what is the likelihood that this particular you will see the electron on the lower left of the screen.
All of a sudden, probability makes sense, since the particular peak of the wave function that allowed for the world you are in is associated with a probability value.
If that value were 9%, you could say that this particular world you inhabit is a relatively rare one.
Excelent review and explanation
Thank you for your comment Kaline! I’m really happy you enjoyed the article!