The “squaring the circle” problem
While I was ferreting out different interpretations of Schism, the one that caught my attention was an interpretation from Dig Interpretations by Jim.
The main idea that Jim proposed in the post was the alchemical concept of “squaring the circle”. I’ll pick this idea and will develop it further here.
There are two uses for the term “squaring the circle”: one mathematical and one spiritual. I’ll start off with the mathematical use (for you numberphobes, please bear with me for a moment, and you’ll see the relevance).
In geometry, “squaring the circle” is described as the ancient Greek problem of creating a square with the same area as a circle. Sounds simple enough right? But wait, there are rules.
You cannot use modern methods to do this, because when the problem was formulated back in ancient Greece, numbers could only be derived using lines and circles with the help of a compass and straightedge (Algebra, which is what is used in mathematics to solve these kind of problems, hadn’t been invented yet; see What is Algebra?).
So the question becomes: can you find a circle and a square that have the same area by only using a compass and a straightedge?
It turns out you can’t: squaring the circle using only a compass and a straightedge is an impossible problem.
To understand why, you’d need to have a fairly decent knowledge of Algebra and Calculus which is beyond the scope of this article.
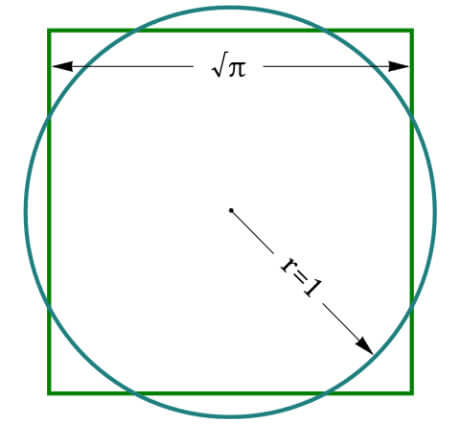
For the present purposes, we will only mention that squaring the circle using a compass and straightedge requires you to construct \( \sqrt{\pi} \), which is impossible.
The area of a square is defined as \( Area\ of\ a\ Square = Side \times Side = s^2 \).
The area of a circle is defined as \( Area\ of\ a\ Circle = \pi r^2 \).
So, you’d need to construct a square so that \( Area\ of\ a\ Square = Area\ of\ a\ Circle \). In mathematical language, \( s^2 = \pi r^2 \).
When you move the \( ^2 \) above \( s \) to the other side of the equation, you get \( s = \sqrt{\pi} \cdot \sqrt{r^2} = \sqrt{\pi} \cdot r \).
So you unavoidably need to construct \( \sqrt{\pi} \) – this is impossible!
The number \( \pi \)
\( \pi \) is a really cool number. It’s irrational, which very loosely means it doesn’t really repeat, or, to be more mathematically precise, it cannot be expressed as a fraction between two integers.
0.5 is a rational number because it can be rewritten as a fraction between two integers (i.e., \( \frac{1}2 \)).
Even a number like 0.33333333… (the three dots mean that it goes on indefinitely) is a rational number because it can be expressed as \( \frac{1}3 \).
\( \pi \), however, is irrational because you cannot represent \( \pi \) as a fraction between two integers.
\( \pi \) starts with 3.1415926535897932384626433832795… and it continues without ever repeating a sequence of numbers.
Now, why is \( \sqrt{\pi} \) so problematic for the squaring the circle problem?
Remember the rules: you can only approach the squaring the circle problem using a compass and straightedge. The numbers you can derive using these rules are called “constructible” numbers.
The issue is that if \( \sqrt{\pi} \) is a constructible number, \( \pi \) will also need to be.
Alas, a mathematician called Ferdinand von Lindemann proved in 1882 that \( \pi \) is not an algebraic number (see What is Algebra?), and therefore it is not a constructible number (all constructible numbers must also be algebraic).
According to Wikipedia Algebra means “reunion of broken parts”. So, in a sense, it means taking something that is incomplete and make it complete.
Take this polynomial equation: \( x + 1 = 4 \)
The goal of algebra is to figure out what the unknown variables in equations are (like the variable \( x \) above). You have something you don’t know (variable \( x \)) and you use Algebra to figure out what it is (in the example above \( x \) is equal to 3, because 3 + 1 = 4). In Algebra you always need to keep one side of the equation equal to the other.
Algebra is very important in real life for describing and modelling things in the real world (like predicting whether an asteroid is likely to crash on Earth).
Algebraic numbers are numbers that cause a polynomial expression to equal 0.
Let’s say you have a number like 0.25. 0.25 is the solution (also called root) of an equation such as \( 100x – 25 = 0 \). Why? Because if you solve the equation for \( x \):
1) \( 100x = 25 \)
2) \( x = 25/100 \)
3) \( x = 0.25 \)
So 0.25 can be expressed in terms of an equation; that is, 0.25 is a solution (or root) to the equation \( 100x – 25 = 0 \).
Therefore 0.25 is said to be an algebraic number, because it causes a polynomial expression (the \( 100x – 25 \) bit) to equal 0.
You can pretty much come up with any number and you’ll see that it is always a solution to a polynomial expression.
Always? Well, no, not always.
It turns out that \( \pi \) is not the solution to any polynomial with integer coefficients.
It doesn’t matter if the equation is \( 1 +x = 1213x^2 + 48x -4 \), or whatever freaky equation you might conceive. There is simply no equation with integer coefficients in which \( x \) will equal \( \pi \).
Transcendental numbers
Mathematicians have a name for a number which is not algebraic (like \( \pi \)). It is called a “transcendental number”! That’s a pretty darn cool name for a number: transcendental!
But, why transcendental?
It’s called transcendental because it transcends the mathematical tools (e.g., Algebra) that humans have created for building numbers and figuring things out.
As opposed to numbers like 10, \( \frac{12}{127} \) or \( \sqrt{2} \), transcendental numbers are numbers we haven’t really created. They exist everywhere in the Universe and we simply don’t have the tools or knowledge to build them.
Even if, after reading this, you feel like sticking your head in the toilet, you have to admit that’s pretty cool, heh?
Contructible numbers are numbers that can be constructed with a compass and straightedge in a finite number of steps. \( 10, 1302, \sqrt{2} \) are all constructible numbers.
Algebraic numbers contain all constructible numbers plus a few more. You can construct \( \sqrt{2} \) using a compass and straightedge, but you cannot construct \( \sqrt[3]{2} \) (cubic root of 2). So anything higher than a square root (\( \sqrt[3]{2}, \sqrt[4]{2}, \sqrt[5]{2} \) and so on) are algebraic (but not constructible numbers).
Both algebraic and constructible numbers are solutions to polynomial equations (check out What is Algebra?).
Transcendental numbers are numbers which are not solutions to any algebraic equation. Some examples of transcendental numbers are \( \pi, e \) and \( \ln 2 \).
Excellent research and concise explanations, your analysis is very accurate given I was able to discern the allegories and symbolism to the same conclusions. There are many facets to the genius of this song and music video that were clearly designed to be played together as inseparable as the constituents of successful synthesis alchemy describes. The fact Maynard’s history reads like a tailored spook (he is one), he declares himself for the legion by signaling the hidden hand, plays from behind a curtain during some shows, the man does a service visualizing these hermetic principles and deep esoteric concepts though at what cost to divulge so clearly I can’t and would rather not imagine.
Hi Ellis! Great comment, thanks for sharing! Indeed, I’ve always felt that the album Lateralus is in itself a description of an entire alchemical journey. However, I also believe that the concepts present in Tool’s songs (including Schism) probably extend beyond Hermeticism and other esoteric teachings. I once watched an interview with Maynard in which he explained quite articulately the nuances of – if my memory doesn’t fail me – Saturn’s orbit, and how it related to “The Grudge”. Tool’s exceptional ability to combine these different pieces of knowledge, and create such harmonious music is truly unique in my view. Entire PhDs could be written about this 🙂