This post is part of a larger deep dive
Curious about the role of the number pi in Pi? Check out Pi Explained!
Or read the full Pi article!
This post is part of a larger deep dive
Curious about the role of the number pi in Pi? Check out Pi Explained!
Or read the full Pi article!
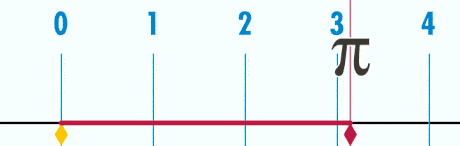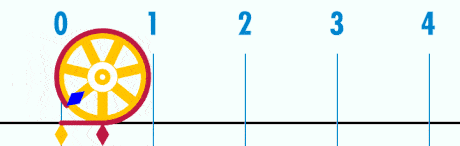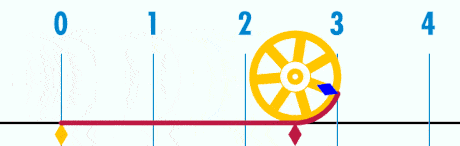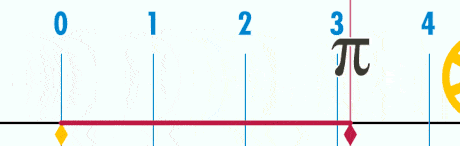

1. \( \pi \) is always equal to the ratio between the circumference of a circle and its diameter
Think about it this way: Imagine a spaghetti string that you join at both tips to form a circle.
Now, with a ruler, measure the length of the spaghetti circle from one side to the other, making sure the ruler passes by the center of the circle – this is the diameter of the circle (let’s say it’s 7 cm).
Next, measure how long the spaghetti string is – this is the circumference of the circle (let’s say it is 22 cm).
If you divide the circumference by the diameter, you get 3.142857…
Well done, you’ve just calculated \( \pi \)! Well, a rounded up version of it.
Another way to think about it is like this: if you divided the spaghetti string into equal parts, each single part would equal exactly \( \pi \)!
Now, the size of the circle doesn’t really matter – by taking the ratio of the circumference to its diameter you will always get \( \pi \).
That means that if you take a circle the size of a pea and measure the ratio of its circumference to its diameter, you will get \( \pi \).
If you take a circle the size of the Earth and measure the ratio of its circumference to its diameter, you will also get \( \pi \).
In fact, take any circle you can think of – a circle the size of the universe for example – measure the ratio of its circumference to its diameter and you are guaranteed to get \( \pi \).
And note, you are not getting an approximation of \( \pi \). If you had access to an absolutely precise measurement tool, you would get the full-blown \( \pi \) with all its inherent oddities (keep on reading to find out which ones).
Isn’t that truly mind-blowing?
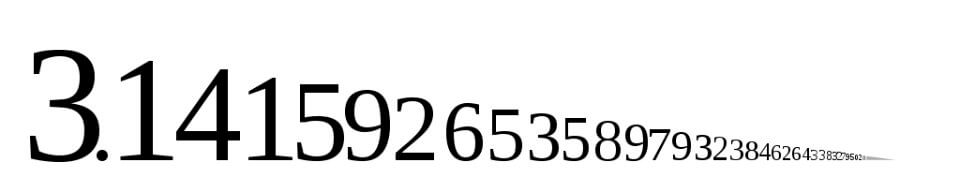
2. \( \pi \) has an infinite number of decimal digits
\( \pi \) is an irrational number, which means that it cannot be written as a fraction between two integers.
A fraction is a number like ½, or -17/32, where the top number is a numerator and the bottom number is the denominator.
For example, 4 can be written as the fraction 8/2. Even a number with an infinite number of decimal places such as 1.3333… (the dots mean that it goes on infinitely) can be represented by the fraction 1/3.
Another example is 1.571428571428571428 571428… . It has an infinite number of decimal places, but it can still be represented by the fraction 11/7. If you look closely the sequence 571428 repeats over and over again.
What about \( \pi \)? It turns out that there aren’t two integers that can make up this number.
Approximations do exist of course: For example, 22/7, but if you looked far enough you would see the same sequence of numbers repeating.
In contrast, the digits of \( \pi \) go on forever in a seemingly random fashion.
As of 2021, the record holder for calculating the longest string of PI digits belongs to Timothy Mullican, who managed to calculate a whopping 50 trillion digits using a computer programme called y-cruncher.

3. \( \pi \) is a transcendental number
Now, \( \pi \) belongs to a more special category of numbers called “transcendental numbers”.
I covered transcendental numbers in another article describing the squaring the circle problem, so be sure to read that as well.
In short, being transcendental means that the number is not the solution to any polynomial equation of the kind \( 2x = 1 \) (numbers that are solutions to polynomial equations are called algebraic numbers; see What is algebra?).
According to Wikipedia Algebra means “reunion of broken parts”. So, in a sense, it means taking something that is incomplete and make it complete.
Take this polynomial equation: \( x + 1 = 4 \)
The goal of algebra is to figure out what the unknown variables in equations are (like the variable \( x \) above). You have something you don’t know (variable \( x \)) and you use Algebra to figure out what it is (in the example above \( x \) is equal to 3, because 3 + 1 = 4). In Algebra you always need to keep one side of the equation equal to the other.
Algebra is very important in real life for describing and modelling things in the real world (like predicting whether an asteroid is likely to crash on Earth).
Algebraic numbers are numbers that cause a polynomial expression to equal 0.
Let’s say you have a number like 0.25. 0.25 is the solution (also called root) of an equation such as \( 100x – 25 = 0 \). Why? Because if you solve the equation for \( x \):
1) \( 100x = 25 \)
2) \( x = 25/100 \)
3) \( x = 0.25 \)
So 0.25 can be expressed in terms of an equation; that is, 0.25 is a solution (or root) to the equation \( 100x – 25 = 0 \).
Therefore 0.25 is said to be an algebraic number, because it causes a polynomial expression (the \( 100x – 25 \) bit) to equal 0.
You can pretty much come up with any number and you’ll see that it is always a solution to a polynomial expression.
Always? Well, no, not always.
It turns out that \( \pi \) is not the solution to any polynomial with integer coefficients.
It doesn’t matter if the equation is \( 1 +x = 1213x^2 + 48x -4 \), or whatever freaky equation you might conceive. There is simply no equation with integer coefficients in which \( x \) will equal \( \pi \).
A mathematician called Ferdinand von Lindemann proved that \( \pi \) is not a constructible number, and if \( \pi \) is not a constructible number, it cannot be algebraic.
Mathematicians baptised non-algebraic numbers with the name “transcendental” because, according to a famous mathematician called Euler, “they transcend the power of algebraic methods”.
Contructible numbers are numbers that can be constructed with a compass and straightedge in a finite number of steps. \( 10, 1302, \sqrt{2} \) are all constructible numbers.
Algebraic numbers contain all constructible numbers plus a few more. You can construct \( \sqrt{2} \) using a compass and straightedge, but you cannot construct \( \sqrt[3]{2} \) (cubic root of 2). So anything higher than a square root (\( \sqrt[3]{2}, \sqrt[4]{2}, \sqrt[5]{2} \) and so on) are algebraic (but not constructible numbers).
Both algebraic and constructible numbers are solutions to algebraic equations (check out What is Algebra?).
Transcendental numbers are numbers which are not solutions to any algebraic equation. Some examples of transcendental numbers are \( \pi, e \) and \(\) \ln 2 [/latex].
Here’s some food for thought:
On the one side, we have a bunch of numbers that are familiar to us and which we know how to “create” and manipulate (i.e., algebraic numbers). These numbers make up most of the numbers we, non-mathematicians, will ever have to deal with in life.
On the other side, there are these obscure numbers which are used to compute all sort of things (for example, area of circles) with very high precision, but of which we have no fricking clue how to construct them.
Keep this thought in mind, because it’s relevant to the analysis of the film!

4. \( \pi \) is related to the golden ratio in numerous ways
The Golden Ratio (also denoted by the greek letter phi: \( \phi \)) is another irrational (but not transcendental) number.
I ask you now, why?
If you read the previous facts above attentively, your answer should be “because, although it cannot be written as a fraction between two integers (therefore, irrational), it is a solution to an algebraic equation (therefore, not transcendental)”.
And you would be correct!
The golden ratio starts with 1.6180339887 … and goes on infinitely. It is the solution to the polynomial equation \( x^2−x−1=0 \), which is why it is not a transcendental number.
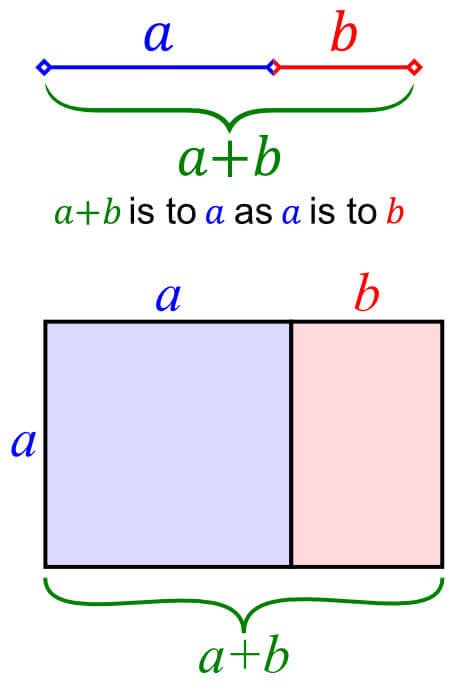
Just as \( \pi \) is the ratio between the circumference to its diameter, the golden ratio is also a ratio. To better explain what that ratio is, look at the left figure above. If the ratio of a+b to a is the same as the ratio of a to b, then the two line segments are in the golden ratio.
Similarly, if the ratio of the longer side of the pink rectangle (i.e., a) to the shorter side of the pink rectangle (i.e., b) is the same as the ratio of the longer side a+b to the shorter side a, then you have a golden rectangle.
Interestingly, there are many ways in which \( \pi \) and the golden ratio are related, although a fairly good level of math skills are required to really understand how.
The point of the paper I linked above is that \( \phi \) (the golden ratio) is the smallest of the Golden Numbers whereas \( \pi \) is related to the largest one.
There are other geometrical and numerical relationships between the two numbers, meaning that the golden ratio is associated with \( \pi \) in meaningful ways, such that you could theoretically get from one number to the other.
Mathematicians have been discovering interesting avenues in which \( \pi \) and the golden ratio are related and they believe that this relationship might be even greater than currently thought.

5. \( \pi \) is very likely a normal number (but not yet proven)
\( \pi \) has an infinite number of decimal places, right? Does that mean it would theoretically be possible to find any imaginable sequence of numbers?
For example, let’s say you wished to determine if the sequence 999999 existed within the decimal digits of \( \pi \).
Indeed, you would be able to find this sequence in the decimal place 762.
Here are the first 1000 digits of \( \pi \):
3.14159265358979323846264338327950288419716939937510
58209749445923078164062862089986280348253421170679
82148086513282306647093844609550582231725359408128
48111745028410270193852110555964462294895493038196
44288109756659334461284756482337867831652712019091
45648566923460348610454326648213393607260249141273
72458700660631558817488152092096282925409171536436
78925903600113305305488204665213841469519415116094
33057270365759591953092186117381932611793105118548
07446237996274956735188575272489122793818301194912
98336733624406566430860213949463952247371907021798
60943702770539217176293176752384674818467669405132
00056812714526356082778577134275778960917363717872
14684409012249534301465495853710507922796892589235
42019956112129021960864034418159813629774771309960
51870721134999999837297804995105973173281609631859
50244594553469083026425223082533446850352619311881
71010003137838752886587533208381420617177669147303
59825349042875546873115956286388235378759375195778
18577805321712268066130019278766111959092164201989
But let’s try more exciting sequences.
For example, let’s say you want to find the sequence 0123456789 somewhere within the decimal expansion of \( \pi \).
Now, if you look at the first 100 decimals, will you find this sequence? Clearly no.
What if you look within the first 1000 decimals? Also no.
Ok, what about 10000? No.
Well, surely in 1000000 (that’s one million numbers)? The answer is still a resounding No!
In fact, you would need to go to the 17.387.594.880th decimal place (that’s more than seventeen billion digits!) to arrive at the 0123456789 sequence.
There are even online tools that help you find sequences within \( \pi \). For example, mypiday is a popular tool to find out where in the number \( \pi \) you birthday date (or any other date for that matter) is located.
This surely begs the question: can we make the point that any combination of numbers that you can think of will be represented somewhere in \( \pi \)?
In order for that to be the case we would need to demonstrate that \( \pi \) is a normal number.
In mathematics, a number is considered normal in the base-10 number system (i.e., numbers with digits that consist of integer values ranging from 0 to 9) if, across its decimal development, there is an equal frequency of the integers 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
Although, it has not yet been proven that \( \pi \) is a normal number, mathematicians suspect that it is.
Consider the table below, which contains the number of times that each number from 0 to 9 shows up within the first billion decimal digits of \( \pi \):
| Decimal digit | Number of times the digit appears |
|---|---|
| 0 | 99.999.485.134 |
| 1 | 99.999.945.664 |
| 2 | 100.000.480.057 |
| 3 | 99.999.787.805 |
| 4 | 100.000.357.857 |
| 5 | 99.999.671.008 |
| 6 | 99.999.807.503 |
| 7 | 99.999.818.723 |
| 8 | 100.000.791.469 |
| 9 | 99.999.854.780 |
| Total | 1.000.000.000.000 |
Sure, there are visible differences in the frequency with which each number appears. However, it’s not a stretch to imagine that as mathematicians keep on discovering more and more \( \pi \) digits, the differences between frequencies will diminish and, who knows, maybe even equalise.
6. \( \pi \) is present in statistics
This is my personal favourite. You might think that \( \pi \), being a number with such odd properties and which is mostly associated with circles, cannot be possibly involved in probability and statistics.
However, it is.
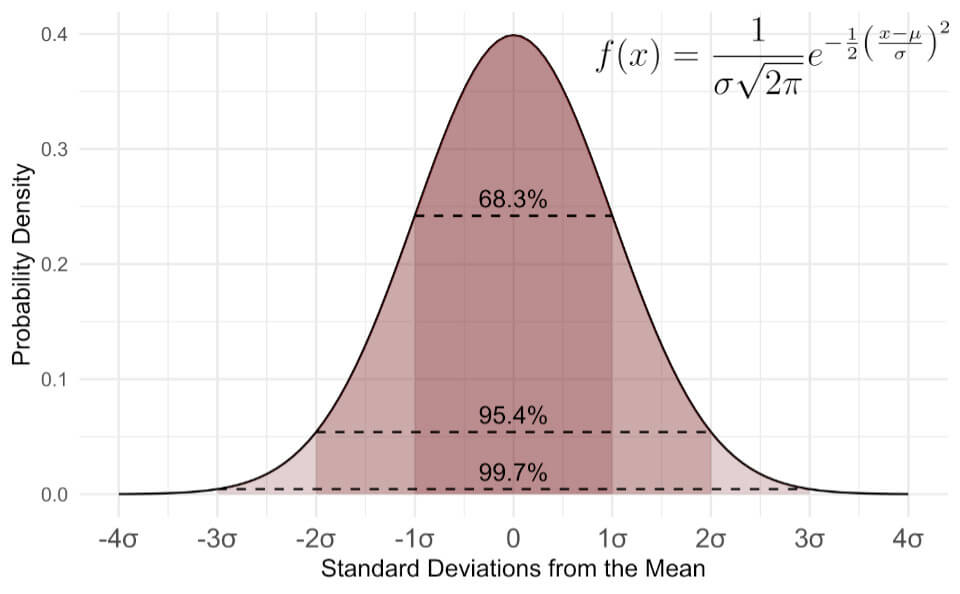
For example, \( \pi \) appears in the normal distribution formula, the most common distribution used in statistics.
The standard normal distribution is a probability distribution formed by continuous variables (things that are measured and can take on an infinite number of values between any two values).
Here’s how it works. Imagine that, for some reason, you wished to know the height of people in New York.
You cannot measure the height of every single person, so you need to select a representative sample.
So, you go out to a busy street in New York and start measuring the height of people you select at random. Let’s say you measure the height of 100 people.
Some people will be tall, some short, but you will be able to calculate an average from those 100 people (say it’s 1.86 m).
However, it could happen that this particular street is frequented mostly by basketball players, so the height you measured might not be very representative of the whole population of New York.
So, you go out to another busy street in New York and measure the height of another 100 people and take the average of all those heights (e.g., 1.70 m). Let’s do this in 1000 streets, each time picking 100 people at random.
Now, if you plot all those 1000 averages (1.86, 1.70, etc), you will get something like a normal distribution plot with its distinctive bell-shape curve (watch this video for a visual explanation of the concept of standard normal distribution). It turns out that many variables are normally distributed if you plot the averages of selected samples as I did with height (e.g., weight, throw of dice, IQ, stock volatility, length of leaves, etc.).
But what does that have to do with \( \pi \)? After all, isn’t \( \pi \) all about circles? What does the standard normal distribution have to do with circles?
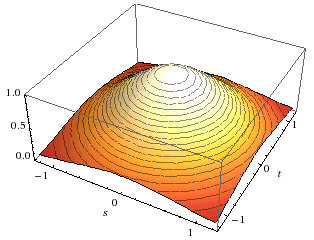
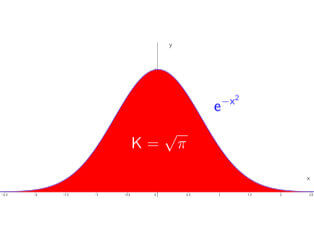
It may not be obvious, but the standard normal distribution is indeed related to circles.
When you square the probability function you go one dimension up. If you look at the 3d plot of the distribution and look at the contour lines you will the circles.
Also, when you center and standardise the curve, such that the mean is zero (\( \mu = 0 \)) and the variance is one (\( \sigma = 1 \)), the area under the curve is equal to \( \sqrt{\pi} \).
There are many more situations in statistics in which \( \pi \) will be involved, such as the probability of two randomly chosen integers being prime numbers between them (which is equal to \( 6/\pi^2 \)), Buffon’s needle problem, tracking population dynamics, etc.
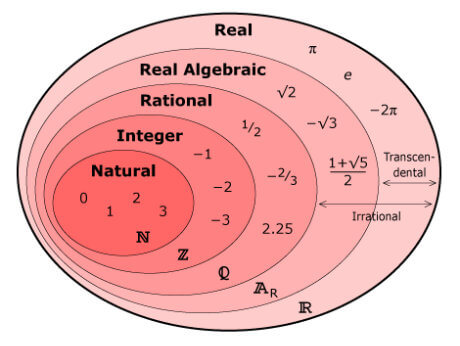
7. \( \pi \) is just one among an infinite number of transcendental numbers
Now that I have hopefully awed you with some fascinating facts about \( \pi \), you might think that \( \pi \) is a truly unique number, perhaps even magical.
Well, it is not.
It turns out that the number \( \pi \) is not really that special. It’s now a mathematical truth that there are way more transcendental numbers than there are algebraic numbers!
If this hasn’t really sunk in, I’ll rephrase it: there are more transcendental numbers (numbers that are so weird that defy our understanding) than numbers we use in our daily lives.
Another way to think about it is to consider the numbers you are familiar with.
So think about the amount of numbers you can imagine: start with 0 and continue with 1, 2, 3, 4, … 100, …, 1000000 and so on until infinity. Well, what I’m saying here is that there are more transcendental numbers than all of those you can count!
For those perspicacious among you, you may have noticed that I wrote that you should count numbers from 0 until infinity.
I then went on saying that there are way more transcendental numbers than those.
But wait a minute! How can there be more transcendental numbers than infinity itself?!
Welcome! You have just entered a truly bizarre corner of mathematics.
First, let’s play a fun game. Let’s say you have one bag containing an infinite number of M&M’s, and you take them out, one by one (no matter how many you take, there’s always one more in the bag).
OK, so let’s count the number of M&M’s that come out of that bag – these are your natural numbers:
Natural numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 … \( \infty \)
Now, I would like to ask you to think of the even numbers only.
Even numbers: 0, 2, 4, 6, 8, 10 … \( \infty \)
My question to you is this: which set do you think is larger: the set of natural numbers or the set of even numbers?
If your answer was “well, obviously there are more natural numbers since they include all even numbers plus all the odd numbers”, you are not alone (I myself once thought that).
However, you are wrong!
It turns out that there are an equal amount of infinite numbers in both sets.
And this is why: If you always multiply each natural number by 2, you will always be able to match it to an even number:
| Natural numbers | 1 | 2 | 3 | 4 | 5 | ∞ |
| Even numbers | 2 (1 x 2) | 4 (2 x 2) | 6 (3 x 2) | 8 (4 x 2) | 10 (5 x 2) | ∞ |
Even if you pick the 10000th M&M you can always match it with 2 x 10000.
If you pick 122.039.482.948.280th M&M you can match it with 2 x 122.039.482.948.280.
It doesn’t matter how many M&M’s you pick, you can always find a match by multiplying a number by 2.
In a moment of sheer brilliance, Georg Cantor even proved that rational and even algebraic numbers are also enumerable. That is, you can always match them one-to-one with natural numbers (watch this easy-to-follow demonstration of how the rational and natural number sets are matched in size).
But what about transcendental numbers? Can they be matched to an infinity set of natural numbers just like the even numbers or the rational numbers?
It turns out they cannot! To understand why, let’s keep it simple and only consider a list of real numbers, \( \mathbb{R} \) (the number set which contain transcendental numbers; see the diagram on the right figure above), that exist between 0 and 1:
| Natural Number | Real Number |
| 0 | 0.194728… |
| 1 | 0.857772… |
| 2 | 0.943289… |
| 3 | 0.409839… |
| 4 | 0.998378… |
| 5 | 0.382922… |
Remember, this is important – you have to think that this list goes on forever, such that you list all real numbers.
Now, you might wonder why can’t we just assign 1 to the first element, 2 to the second, 3 to the third and so on, just like we did when we matched the natural with the even numbers.
To show you why this doesn’t work for the real numbers, let’s take the first element of the first number, the second element of the second number and so on.
Your number will be 0.153872….
Now, let’s add 1 to each digit in your number and the result will be 0.264983….
Is this number on your list? You guessed it, it isn’t.
You can go ahead and add the number to the list if you liked, but that won’t matter. I can do this game over and over again with the numbers you add to the list.
In fact, there would be an infinite amount of numbers missing! I can come up with infinite ways to make a number that isn’t on your list – I added 1 in the example above, but I can also add 2, subtract 8.2, multiply by 0.1938164, and so on and so on – it will never ever stop.
Now, what is the implication of this? The implication is that there are way, way, way more numbers that lie between 0 and 1 than there are natural numbers (1,2,3,4, … infinity)!
As opposed to algebraic numbers, which comprise a countable infinite set (you can match them one-to-one to natural numbers), transcendental numbers comprise an uncountable infinite set (there are too many of them to be able to match them one-on-one to natural numbers).
In fact, consider this: if you were to pick a number randomly from all real numbers, the probability that you picked a transcendental number would be 1! That’s it: 1! That means you are guaranteed to pick a transcendental number – that’s just how many there are!
I find this utterly mind-boggling, because mathematicians actually only know a handful transcendental numbers (see the current full list of numbers that have been proven to be transcendental).
However, it has been proven that they amount to a much, much, much larger quantity than algebraic numbers.
Masterpiece
Hermetic Interpretation
Artistically speaking, the math does not need to make sense. Whatever it is that Max has discovered, people in the world of finance (material world) have noticed his work and are literally following him. And people from the world of religion (spiritual world) have also noticed his work and are following him. The Wall Street folks want to rule the world financially while the religious group admit to wanting to have power as well. The rabbi gives Max the information he needed: what the number is for. The rabbi notes that he and Max have the same last name, “Cohen”, meaning “priest”. But Max’s first name is “Max”, which means “high”. Max is the High Priest, the only one who can be trusted with the Holy Name of God, which it is his responsibility to utter in the Holy of Holies, just once, in ORDER to move history along to the time of the Messiah’s coming. Max is not blubbering random numbers as he destroys his computer, but the Name of God. Max accomplished this high and holy task, but humbly, with no thought of reward for himself, other than the freedom to live an ordinary life, which he wins by, as you said, “destroying the evidence”, including the evidence inside his own head, which they could torture him for, but he tortures himself first and destroys the part of his brain that appears to be the source of all the commotion. Great movie. Max is a hero, not a psycho. You all get it wrong.
You could also use some writing classes. Your grammar needs some work.
Hi Natasha,
Thank you for your comment.
Actually, I mostly agree with your interpretation. If my analysis somehow came out as suggesting that Max was a “psycho”, that was unintentional. The “insanity” I attributed to Max was described in the context of Max’s realisation of some fundamental truth (be that the true name of God, the source of all consciousness, the mathematical pattern governing every natural phenonmenon, or something else) that was presumably too much for a human mind to handle, no matter how mathematically- or spiritually-trained one would be.
Aronofsky was proposefully ambiguous (as he always is with his films) regarding Max’s discovery at the end, but he left subtle clues throughout the movie (such as the title in the journal where Max writes down the number: “Only God is Perfect”). One important clue was in the audio commentary by Aronofsky himself, where he mentioned he wanted the actor portraying Max to appear naked while reciting the numbers close to the end of the film. To me, it clearly suggests there is something transcendental about Max’s state of mind at that point, which is the reason I’m also leaning towards the idea that Max was a genius, not a psycho.
Wow, what an incredibly well-written article. Most compelling movie deep dive (and then some) I’ve read in a long time.
Hi birdobserver,
Many thanks for your comment, and I’m very happy you enjoyed the article!
👏
Thank you! I’m glad you liked the article! 🙂
You’re amazing, keep up the brilliant work